The State of Quantum RAM: A new enlightening Investigation

The realization of quantum RAM aka QRAM would be a game changer for the quantum industry. Very promising proposals almost two decades ago have inspired quantum algorithm engineers at first. But the lack of success stories has disillusioned many by now. Information about the state of QRAM is rare and hardly known. A highly interesting, recent preprint brings light into the dark: A thorough investigation about the state of quantum RAM and its fundamental challenges. Yet, the text is also long and rich of technical details. In this article you will find an overview of my lessons learned from studying the survey. I have simplified the selected highlights to help you getting into the subject yourself.

Image by Gerd Altmann from Pixabay

QRAM: The missing Game Changer

Data plays a central role in universal computation. It is data that breathes life into most algorithms. Making data memory fast and randomly accessible, was a major step in the evolution of digital computers: RAM. The same holds for quantum computation. Unfortunately here, the situation for quantum RAM aka QRAM is even more complicated:

Imagine a superfast quantum algorithm, that has to perform a lookup on a “table” $ T $ of $ N = 2^n $ bits of data. We want to store this table and make it randomly accessible for a quantum computer. In the quantum world a QRAM-lookup of the (classical) data has to perform the following operation on an address register A and an output register O

$$
\lvert i \rangle_A \lvert 0 \rangle_O \longrightarrow \lvert i \rangle_A \lvert T_i \rangle_O
$$

A simple circuit implementation to access the table, is a series of controlled operations of the type

IF address register = i: 
   THEN add T_i to the output register

For such a lookup an order of $ O(N) $ gates are executed altogether. But this would destroy any superpolynomial speedup in $ N $ of the algorithm!

So, to maintain a superfast quantum speedup, you need to a have superefficient QRAM. Exactly such a QRAM was sketched in the ground breaking “bucket-brigade”-paper by Giovannetti, Lloyd and Maccone in 2008 ⁱ – more about this later. Afterwards, QRAM played a key role in various superfast quantum algorithms. The most famous among them is probably the HHL algorithm for solving equations in linear algebra, which achieves a runtime of $ O(log N) $. Along, QRAM was one of the concepts that helped to drive the first wave of quantum machine learning algorithms. But the problem was: The physical realization of the “bucket-brigade”-QRAM was not in sight. This and other constraints led Scott Aaronson to demand “Quantum Machine Learning Algorithms: Read the Fine Print” in 2015 ⁱⁱ. In it, he also coined the term “passive” QRAM. Afterwards not only the first wave of quantum machine learning algorithms ebbed significantly. Also, the enthusiasm for QRAM dropped.

“QRAM: A Survey and Critique”: Lifting the Fog

In my impression the situation has not changed and is still … very foggy. Once in a while I hear the rather wistful question “… and what about QRAM?”, but not even the hardware teams seem to have a real answer. This is all very disappointing.

Therefore, I was very surprised to stumble over a recent preprint from May 2023 by Samuel Jaques and Arthur Rattew (University of Oxford) with a pretty remarkable rating of 58 on Scirate ⁱⁱⁱ. Its title “QRAM: A Survey and Critique” immediately got me hooked.

The study is a thorough investigation about the concepts, challenges and use cases for QRAM. It discusses several strategies of hardware and software implementations. Also, the authors propose regimes, where QRAM could work and encourage scenarios for further research. The preprint has finally given me an understanding of the fundamental problems, that the realization of QRAM faces. But I was also surprised to find out, that there exist promising works, that incorporate a realistic concept of QRAM.

As a survey of various papers the preprint is a broad collection of technical details and even the main text is about 30 pages long. So, if you are also curious about the subject but would like to speed up things for you, then in the following text you will find a personal overview of my lessons learned from reading. For the purpose of this article I have rearranged and simplified the selected highlights of the work. This should help you getting started with the survey yourself.

The Bucket-Brigade: The Mother of all QRAM

But first step back for a second to the mother of all quantum RAM: The “bucket-brigade”. The original work also sketches a “proof of principle” implementation. This is how it works:

A binary tree in general
Image by Rune Magnussen via Wikimedia

The implementation is a binary tree of trapped ions or atoms. Each atom is restricted to three states “wait”, “left” and “right”. Thus, each node is a “qutrit”. In the “wait” state, the node is inactive. This is the initial state of all nodes. The excited states “left” and “right” couple to the left and right spatial direction of the next layer. The coupling is mediated through photons in the following way:

If a quantum processor needs to access an address encoded as qubits in an address register, each qubit in the address register generates a photon, starting from most significant to least significant qubit. The state of the qubit is translated into the photon’s polarisation states $ \lvert left \rangle_P$ and $ \lvert right \rangle_P$. If this photon reaches a node, the following can happen:

• • $ \lvert W \rangle_A $: If the node’s atom is in the wait-state, the photon gets absorbed and generates an excited state $ \lvert L \rangle_A $ or $ \lvert R \rangle_A $ depending on its own polarization

  • $ \lvert L \rangle_A $: If the node’s atom is in the left-state, the photon is deflected to the node on the left spatial direction of the next layer, using stimulated Raman emission, without changing its own state or the state of the forwarding atom. At the next node, the same three cases are possible.

  • $ \lvert R \rangle_A $: If the atom is in the right-state, the photon is deflected to the node on the right spatial direction of the next layer without changing states as above. Again, at the next node, the same three cases are possible.

This will initialize a path of active nodes through the binary tree according to the qubits in the address register from most significant to least significant: A bucket-brigade. If all address qubits are sent this way, the data bit in the leaf is read out by generating a polarized photon which gets routed in the same way but from bottom to top.

A nice feature of the bucket-brigade model is that an error in any node just logarithmically effects the outcome, as only the nodes in the active path are able to propagate errors all the way up. The authors state, that this may be improved even further by error correcting the top layers (somehow) as errors at this stage have greater impact.

As appealing as the bucket-brigade is, it also illustrates all the problems that challenges the realization of QRAM.

Active versus Passive Gate-QRAM

Gate-QRAM

In their preprint Jaques and Rattew call a specialized hardware device as the one described above “gate-QRAM“. It is absolutely crucial that such a device executes with as less interventions as possible. Ideally such a system evolves passively through a single time-independent Hamiltonian. The authors call this “ballistically” and compare it to a Galton box

Galton box, an example of a “ballistical” device
Image by Rodrigo Argenton via Wikimedia

They formulate the key argument of their work as follows:

“In the active model, there is a powerful opportunity cost argument: in many applications, one could repurpose the control hardware for the qubits in the QRAM (or the qubits themselves) to run an extremely parallel classical algorithm to achieve the same results just as fast.”. If gate QRAM needs $O(N)$ interventions, then it is qualitatively no better than “circuit-QRAM“, a software implementation as the simple one sketched above (more about this further down). For example, the original bucket-brigade-paper suggests stimulated Raman emission for the atom-photon interactions, which Jaques and Rattew judge as an active device. More generally, the preprint formalizes the problem of active interventions in a theorem that indicates, that there is trade-off of the number of interventions against time and energy: If one is fixed, the other must grow with the QRAM-size.

Note, that this requirement not only counts for routing to the correct memory cell, but also for reading out the data. As the authors state “For perspective, if we lose a single visible photon’s worth of energy for every bit in memory for each access, accessing $2^{50}$ bits costs about 1 kJ. As we move into cryptographic scales, QRAM becomes clearly absurd. A single photon’s worth of energy per bit means 1 giga-Joule per access if we have $ 2^{80} $ bits” (more about these applications and memory scales later).

Reversibility

A purely passive gate-QRAM that is driven by a single time-independent Hamiltonian, would be reversible. Thus, any implementation faces the challenge that excited states relax to lower energy states. Nodes will need to be carefully engineered to control this without interventions. Yet, as for the bucket-brigade, relaxation is also required: After each QRAM readout the nodes need to turn into the initial waiting-state. This may be achieved, if the emission times of the atoms in the layers at the bottom are designed to be shorter, than the once further up the active path. Thus, the last atom would emit the first photon which would be neatly routed along the remaining active path. In this sense, atom by atom would relax, emit photons which are correctly routed and the address register would restore. For this to happen, emission and absorption errors need to be extremely small. The preprint quantifies this further. Because of all these challenges, the authors concludes “If this interaction problem is solved, the QRAM routing tree looks like a full-fledged trapped ion quantum computer”.

Please note, that besides all of these challenges, we are not even talking about coherence times yet!

Proposals for physical QRAM-Implementations

The authors describe several proposals in the literature for implementing bucket-brigade-QRAM. Unfortunately, according to Jaques and Rattew, they all fall short in some way or the other as outlined. In particular, besides the original design with trapped ions, they explain approaches using

• • Transmons
  • Photonic transistors
  • Heralded Routers
  • Photonic CNOT

Among these, the Transmon-proposal seems most promising, as it provides enough parameters to tune the nodes for constructing a truly passive device ^iv.

Besides these, the authors describe other QRAM-designs in the literature, that do not follow the bucket-brigade approach. Again, they also explain in detail, why they fail to provide a passive device:

• • Time-bins
  • Quantum Optical Fanout
  • Phase Gate Fanout
  • Derangement Codes

QRAM errors

From the previous arguments we should realize by now, that error correcting the individual nodes in gate-QRAM will essential copy error corrected software implementations. So Jaques and Rattew propose to interpret gate-QRAM as a single physical gate and to correct its output errors. This imposes certain problems, as this physical device would need to couple to logical qubits. As the authors outline, it its unlikely, that the QRAM-gate acts transversal to the error correcting code in the quantum computer. This means, we cannot just couple the noisy QRAM to the physical qubits and the error correcting code will do the rest for us. Instead they propose a distillation of the QRAM-gate, very much like the distillation of T-gates in the surface code. This means, we use $ d $ calls to the noisy QRAM-gate and distill these outcomes to a state of much higher fidelity. Unfortunately, as the authors argue in a theorem, to achieve a high fidelity state, $ d $ has to grow quadratically with the size of the QRAM. But this is asymptotically no better than error corrected circuit-QRAM aka software implementations.

Applications for QRAM and their Scaling

Image by Mudassar Iqbal from Pixabay

The preprint lists several interesting applications for QRAM along with numerous references. To my surprise, their focus is not on data for context (like big data, machine learning, finance, …). Instead these works rather use QRAM to speed up quantum calculations. Some of them incorporate optimized software implementation for QRAM (Jaques and Rattew call these “circuit-QRAM”) which are used to compile detailed resource estimations of the use cases. The preprint summarizes the QRAM-specific scaling of these studies and outlines details about the QRAM-implementations.

Optimizing calculations

As the authors state for the the first application:

“Optimizing calculations. Many quantum algorithms perform complicated classical functions in superposition, such as modular exponentiation in Shor’s algorithm or inverse square roots in chemistry problems. Recent techniques … choose instead to classically precompute the result for a large portion of inputs, and then use … [QRAM] to look up the result.”.

For instance, in one referenced paper Google’s Craig Gidney uses a technique called “windowed arithmetics” ^v. In there, he trades controlled arithmetic calculations, which are controlled by a qubit register, by using the same register as an address register for a QRAM-lookup. The operations are merged into a single windowed batch lookup on the QRAM. Gidney gives the following motivation for this procedure:

“At first glance, this may seem like a bad idea. This optimization saves twenty [quantum] multiplications, but generating the lookup circuit is going to require classically computing all $ 2^{20} $ possible results and so will take millions of multiplications. But physical qubits are noisy …, and quantum error correction is expensive … . Unless huge advances are made on these problems, fault tolerant quantum computers will be at least a billion times less efficient than classical computers on an operation-by-operation basis. Given the current state of the art, trading twenty quantum multiplications for a measly million classical multiplications is a great deal.”.

By the way, see my article Does Quadratic Quantum Speedup have a problem? to find out more about the problems, that Gidney is referring to.

Jaques and Rattew state the following nice aspect about windowed modular exponentiation: Shor’s algorithm requires only about 17 applications of QRAM-lookups. So we could afford much higher error rates for each QRAM-lookup than for other gates. Note, that passive gate-QRAM would only speed up this type of optimization, if the table of data will not have to be regenerated for each application. This could be the case for Google’s qubitization-paper ^vi, which uses QRAM to look up the value of a function of the Coulumb potential.

In the exemplary papers the QRAM-size $ N $ is rather manageable (around $ 2^{15} $ to $2^{25} $). This means, that in these cases a lookup cost of $ O(N) $ is actually acceptable and the studies still achieve an overall quantum advantage.

Other applications

Another QRAM-application that the authors of the preprint give is the “Dihedral Hidden Subgroup”. And again by the way, see my general introduction for these kind of problems From Shor to the Quantum Hidden Subgroup Problem – A jumpstart. In my article I also introduce Greg Kuperberg’s sieve-algorithm for solving the Dihedral Hidden Subgroup – problem. Almost ten years later he published an improved algorithm that relies an QRAM ^vii. The goal of the algorithm is to construct an optimized “phase vector state” to read off the characteristics of the hidden subgroup.

The new algorithm uses a table of “phase multipliers” constructed from previous measurements. Using QRAM-lookups Kuperberg’s iteratively constructs improved phase vector states from the previous vector states that came along with the previous measurements. For such cryptographic applications Jaques and Rattew give a mid sized scaling of $ 2^{18} $ to $ 2^{51} $ bits. In these regimes a passive gate-QRAM would start to speed up calculations significantly.

Much worse QRAM-scalings are needed for attacks on quantum-safe cryptography. For these applications, the preprint gives a range of $ 2^{49} $ up to $ 2^{93} $ bits. As these also tend to find a single element in memory, the error rate needs to be extraordinarily high. This is also the case for a Grover-search on a database.

These regimes also indicate, at which scales context data may be loaded into the quantum computer using circuit-QRAM or active gate-QRAM without ruining the overall performance of a fast quantum algorithm. In the case of quantum linear algebra, such as the HHL algorithm, the preprint presents a detailed case study by considering all kinds of runtime costs (obvious and hidden).

Circuit-QRAM

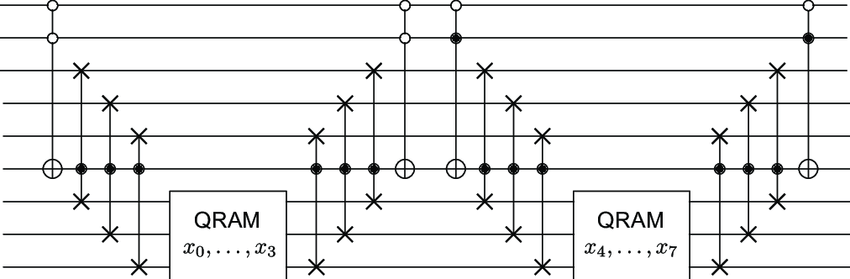
Credits Hann, Connor & Lee, Gideon & Girvin, Steven & Jiang, Liang. (2020)
The resilience of quantum random access memory to generic noise. / CC BY 4.0

From the arguments in the previous sections it should be obvious, that the authors of the preprint have little hope for the case of truly passive gate-QRAM. Yet in the last section it also became apparent, that there exist regimes, for which software implemented QRAM could be sufficient. As mentioned, the work provides detailed description of various implementations, with different pros and cons regarding gate complexity, depth, T-gate count, space usage and error scaling.

A bucket-brigade implementation

For instance a bucket-brigade may be implemented by using two qubits for each node in the tree: A routing qubit and a controlling qubit. The routing qubit takes the role of the photon, which is routed along the active path. The controlling qubit manages the activation state of each node and controls the routing: For each node the routing qubit is swapped either to the left or the right routing qubit in the next layer of the active path. This swapping is controlled by the controlling qubit of the node. If the routing qubit reaches an inactive layer, it is not swapped to the routing qubit but to the controlling qubit of the inactive node, thus making it active and controlling the routing of the subsequent routing qubits. After the full path is activated, the data qubit of the leaf controls a CNOT on the routing qubit of the last layer. This routing qubit is then swapped layer by layer as before, yet from bottom to top. This implementation has a gate count of $ O(N log N) $ and its depth is $ O(log N) $. As described above for the physical implementation, the error rate per node may be relatively large compared to simpler QRAM-implementations. Generally, one would expect error rates of order $ O(1/N) $.

Have fun reading

You will find even more aspects in the survey, that I did not cover (e.g. a detailed comparison with classical RAM and the case study about quantum linear algebra) – so, check out the preprint yourself. I should mention, that at first, it took me a while to get into the work due to some technical formalities: The preprint starts by proposing a general naming scheme for QRAM (following Greg Kuperberg’s paper) as this is used rather inconsistently throughout the literature. Thus, the authors use the terms QRACM or QRAQM for quantumly addressable (in superposition) classical data or quantum data ^viii. Although Samuel Jaques was kind enough to provide further explanations to me, I decided to use the term QRAM instead in my article and keep things simple. Also, the authors themselves state, that at the end the difference between QRACM and QRAQM may be neglected, as the addressing and routing works the same for either case and is the main challenge for QRAM. In this sense, they also use QRAM as a generic term.

Footnotes