Quantum chemistry is one of the top most promising applications for quantum computing – due to the quantum nature of chemical calculations. Most likely, the success in quantum chemistry will serve as a reliable “early-alerting indicator” for other potential applications. Thus, staying up to date to the developments in chemistry is important for the entire quantum computing community!
But papers and preprints for chemical algorithms and use cases are packed with highly technical concepts and terms from traditional quantum chemistry. This is bad news for every quantum computing enthusiast without a training in computational chemistry: Filling all your “knowledge-gaps” means studying it from the ground up – a branch of science that has been making progress for a whole century!
The following two articles are a condensed but still pretty detailed introduction to many concepts and methods of quantum chemistry that are relevant for quantum computing. They are a quick guide, that helps you to get into the field and start tackling further literature and quantum computing papers yourself.

Contents
- 1 Introduction
- 2 Atoms, Spin and Atomic orbitals
- 3 Atomic Bonds and Molecules
- 4 The Hartree-Fock method and a Basis-Set Introduction
- 5 Post-Hartree-Fock I: From Configuration Interaction to Multireference
- 5.1 About the error of the Hartree-Fock method
- 5.2 Full Configuration Interaction FCI in a Nutshell
- 5.3 Configuration State Functions CSF in Quantum Chemistry
- 5.4 Truncated Configuration Interaction CISD, CISDT, … and size inconsistency
- 5.5 Single-Reference and Multi-Reference systems in Quantum Chemistry
- 5.6 The Multiconfiguration Self Consistent Field method MCSCF I
- 5.7 My follow-up article: More about Post-Hartree-Fock methods
- 6 Appendix 1: Derivation of the Hartree-Fock equations and the Fock operator
- 7 Footnotes
1 Introduction
1.1 Quantum chemistry as an “early-alerting indicator”
If you are staying up to date to the developments in quantum computing, you are used to check out preprints and papers, that your social media channels, SciRate and the science news recommend to you. There is one area of application, that I pay attention to in particular – the quantum computing papers, which deal with quantum chemistry:
Because of its quantum nature, quantum chemistry has been one of the top most promising applications of quantum computing since its early days. May-be even the top most. Also, there exists a huge industry, that is always eager to explore and incorporate new methods to boost research and development.
We all know, that memory for input data is limited for use cases in quantum computing. No problem for quantum chemistry: There exists a super-efficient mapping from molecular spin-orbitals to qubits.
Plus, classical computations in quantum chemistry are extremely costly. Exact methods have an exponential scaling in the number of molecular orbitals. Although many very sophisticated approximation techniques exist for digital computation, their polynomial scaling quickly gets very bad, once we aim for higher accuracy. For chemical systems, that show a multireference character, even simple examples quickly get out of scope.
My opinion about chemistry and quantum computing is: If we can’t make it there, we can’t make it anywhere.
1.2 Learning quantum chemistry

But if you have ever looked into quantum computing papers for chemistry, you have noticed, that they are packed with many highly technical terms and concepts from traditional quantum chemistry. Any attempt to fill your “knowledge-gaps” by searching the internet, is doomed to fail :-(. You will soon realize, that there are just too many of those gaps. But, honestly, who are you kidding? Quantum chemistry has been around since the birth of quantum mechanics itself. It is a very mature and rich branch of science.
So there is no way around, you have to study it from the ground up! But even worse: Quantum computing enters the ring with the very best and cutting-edge methods in digital quantum chemistry. So you even need to study very advanced stuff. Feeling frustrated? See it this way: What a challenge! 🙂
Fortunately, there is a wide range of literature and lectures out there on the public internet. The challenge is rather to pick out the right one. E.g. I recommend a thourough lecture series on chemistry on YouTube by Christopher Cramer. He is also the author of a well-known textbook. For quantum computing, we only focus on parts of it. There is also a lot of public literature available on chem.libretexts.org. Specifically, for this article, I have used a very detailed online-textbook by Simons and Nichols.
Introductions to graduate level and even more advanced topics are harder to find online. I have found a very insightful introduction to the correlation consistent basis sets, written by a main contributor to the program. I have also dug out a very nice PhD-thesis about the multiconfiguration self consistent field methods, that demonstrates orbital optimization explicitly.
1.3 About these two articles
Quite a while ago, I started my personal “tour de chemistry” and I can tell you: If you manage to take your time, you will get fascinated about all the smart chemical concepts that theorists came up with during one century of scientific work. In the following two articles, I pass over my lessons learned to those who want to evaluate the progress of quantum computing in quantum chemistry themselves: A quick-tour through the most important traditional concepts and methods, that are relevant to us.
I tried to write brief if possible and precise, if I found it necessary. At the end, the articles got way more extensive and detailed than I had originally planned. So, this report does not only prepare you for the next buzz-word-bingo … for this purpose all important terms are highlighted in bold 😉. It should also give you a good understanding of the topics, their connections and even sketches mathematical derivations. Of course, I provide numerous references for getting deeper into topics.
Unlike my other articles, these two deal with quantum computing itself only briefly: I think, there are already many nice introductions for quantum algorithms in chemistry. Yet, they all heavily rely on concepts from traditional quantum chemistry. Without the necessary chemical training, this leaves you with a sense of confusion at the end of the day. My article series focuses on these underlying topics.
To be specific, you will learn more about the following subjects:
This article / Part I: An introduction to the basic concepts
- The Hamiltonian of the H-atom
- Symmetry and angular momentum, the strange “spin”
- Atomic quantum numbers
- Spatial atomic orbitals and spin-orbitals
- Multi-electron atoms
- Atomic bonds and molecular orbitals
- “Ab initio”, the importance of chemical accuracy and the “1.36 rule“
- The Born-Oppenheimer approximation and the potential energy surface
- Slater determinants, the Hartree-Fock-equation and canonical molecular orbitals
- A self consistent field method and the Roothaan-Hall solutions
- Introduction to Gaussian type basis sets and the correlation consistent program
- About correlations and Post-Hartree-Fock
- Single- and Multi-reference
- Full configuration interaction, configuration state functions and size consistency
Article / Part II: More about Post-Hartree-Fock methods
- Introduction to Second Quantization
- A detour to quantum computing for chemistry: The Jordan-Wigner transformation, the Aspuru-Guzik / Whitfield-method and a roadblock for VQE
- Multireference, the MCSCF- and CASSCF-methods and optimizing molecular orbitals
- Coupled Cluster theory and Coupled Cluster Pertubation theory
- Møller-Plesset perturbation theory
- CCSD(T): The “gold standard” of quantum chemistry and some concrete equations for its 4th and 5th order corrections
- DMRG, exploiting quasi 1-dimensional systems
- Scalings, examples / limits
Okay, enough for the introduction.
Let’s do some chemistry!
2 Atoms, Spin and Atomic orbitals
2.1 Let‘s start at the very beginning
First there was light …
… and one second after the Big Bang the plasma of free quarks and gluons combined to protons and neutrons. Three minutes afterwards, the synthesis of the light nuclei was finished. Yet it took the early universe another 380,000 years expanding and cooling to condense the particle soup into atoms: Negatively charged and very light electrons, that orbit a positively charged and very heavy atomic nucleus. For each atom the number of electrons equal the integer charging $Z$ of the nucleus.
The binding of the electrons established discrete energy levels, making the early foggy universe suddenly transparent to almost all wave lengths of light. Later, stars and supernovas created the heavier nuclei and atoms.
2.2 The Schrödinger equation of the Hydrogen atom
How does the electronic structure of the atoms look like? For atoms with $ Z < 40 $, we can neglect relativistic effects. In this case all properties and dynamics of the electrons are governed by the famous Schrödinger equation:
\begin{gather}
E \lvert \psi_e \rangle = H \lvert \psi_e \rangle
\end{gather}
with the energy levels $E$ and the Hamilton operator (Hamiltonian). This equation can be solved exactly for the most simple type of atom: A hydrogen-like atom with only a single electron. In this case, the Hamiltonian gives i1 :
\begin{gather}
H = \frac{P^2}{2m_e} -\frac{Ze^2}{r}
\end{gather}
In this equation,
- $ P $ is the 3 dimensional momentum operator of the electron
- $ r $ is the scalar, radial distance of the electron from the center
- $ m_e $ the electron’s mass
- and $e$ its charge
The second term of the Hamiltonian is called the Coulomb-potential, the electrostatic attraction between the electron and the nucleus. For spherical problems, the momentum $P$ may be expressed by a radial component and the angular momentum operator $L$ with individual spatial components $L_x, L_y, L_z$:
\begin{gather}
H = \frac{P_r^2}{2m_e} + \frac{L^2}{2m_e r^2} – \frac{Ze^2}{r}
\end{gather}
The Schrödinger equation may be simplified by an ansatz using an outer product with a radial and an angular component for the electron state $ \lvert \psi_e \rangle = \lvert u_r \rangle \otimes \lvert Y \rangle $ with
\begin{align}
L^2 \lvert Y \rangle &= \hbar^2 l(l+1) \lvert Y \rangle \\
\text{and} \\
E \lvert u_r \rangle &= \left( \frac{P_r^2}{2m_e} + \frac{\hbar^2 l(l+1)}{2m_e r^2} – \frac{Ze^2}{r} \right) \lvert u_r \rangle
\end{align}
From a mathematical standpoint, especially the first eigenequation is highly interesting: In physics, there is a deep connection between a spatial symmetry of the system and an associated conserved momentum. For example, a spherical and centralized system like an atom has a rotational symmetry with a conserved angular momentum.
Further, the spatial components $L_x, L_y, L_z$ of the angular momentum must follow the same commutation rules as the rotational “Lie algebra” $ [L_i, L_j] = i \epsilon_{ijk} \hbar \cdot L_k $. Its “irreducable representations” in our Hilbert space are exactly the eigenstates of the first equation. I outline this in more detail in the footnotes i2.
Accordingly, these eigenstates may be labeled by the magnitude of the angular momentum and its orientation in the z-direction:
\begin{align}
L^2 \lvert l, m \rangle &= \hbar^2 l(l+1) \lvert l, m \rangle \\
\text{and} \\
L_z \lvert l, m \rangle &= \hbar m \lvert l, m \rangle \quad \text{with} -l\le m \le +l
\end{align}
2.3 Quantum Numbers in Quantum Chemistry
$ l $ and $ m $ are integer quantum numbers.
The radial component of our ansatz above establishes the different energy levels $ E_n $ and introduces the third quantum number of the atom’s states, the principal quantum number $ n $ with
\begin{gather}
n = 1, 2, 3, … \\
\text{and} \\
0 \le l < n
\end{gather}
In particular the energy levels only depend on $ n $ and not on the angular properties.
2.4 Atomic Orbitals in a Nutshell
So far we have not restricted our discussion to a certain basis. But usually, when working with atoms, we use a continuous, spatial basis either in euclidean coordinates $ \lvert x, y, z \rangle $ or polar coordinates $ \lvert r, \theta, \varphi \rangle $. Note this crucial difference to quantum computation: There, we have a discrete basis, like the computational basis, and our state vector has a finite set of indices. Here, our state vector turns into a wavefunction with continuous variables, an infinite domain. Likewise, the wavefunction’s Hilbert space is infinite dimensional.
To be exact: Its Hilbert space is the space of square Lebesgue-integrable functions and its inner product is
\begin{gather}
\langle \phi \lvert \psi \rangle = \int d^3x \cdot \phi(x)^* \psi(x)
\end{gather}
In the polar basis, our states are expressed as $ u_n(r) = \langle r \lvert u_n \rangle $, $ Y_{l,m}(\theta, \varphi) = \langle \theta, \varphi \lvert l, m \rangle $ and the operator equations are formulated as partial differential equation of these wavefunctions. And if you do a whole bunch of sophisticated PDE-solving you may actually express the eigenfunctions in an analytical form. The $Y_{l,m}(\theta, \varphi)$ are called “spherical harmonics”.
The $ \psi_{n,l,m}(r, \theta, \varphi) = u_n(r) \cdot Y_{l,m}(\theta, \varphi) $ are the (spatial) atomic orbitals. Their shell is governed by the principal number $n$.
Their energy levels correspond to lines measured in spectroscopical experiments. In this tradition, for each $ n $, the atomic orbitals are additionally grouped into the following subshells:
- s / sharp: $l=0$ and $m=0$
- p / principle: $l=1$ and $ m= -1, 0 ,+1$
- d / diffuse: $l=2$ and $ m=-2, -1, 0, +1, +2 $
- f / fundamental: $l=3$ and $ m=-3, -2, -1, 0, +1, +2, +3 $
These subshells correspond to the $l$-subspaces of the angular irreducable representations mentioned in the footnotes. And we note, that their dimension is always odd!
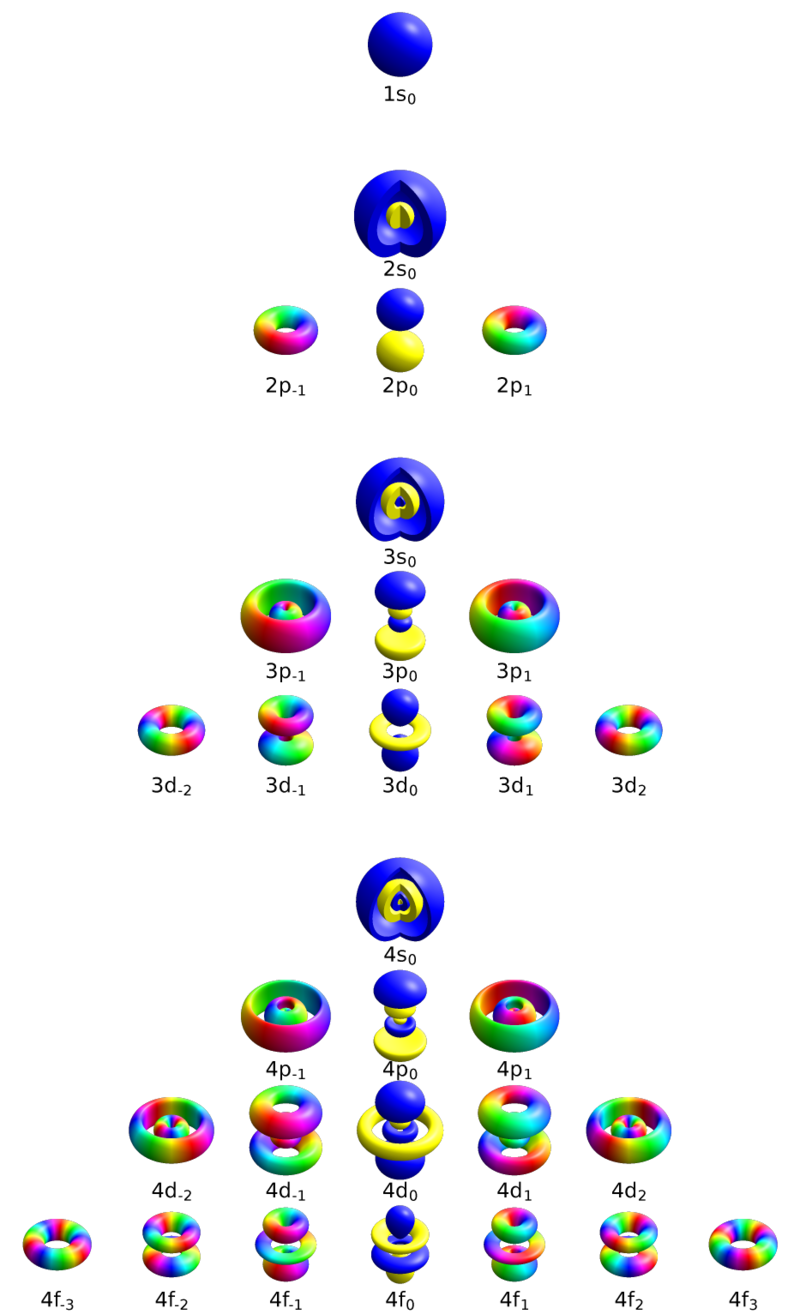
By Geek3 – Own work, Created with hydrogen 1.1, CC BY-SA 4.0 via Wikimedia,
The color depicts the complex-valued phase of the orbital.
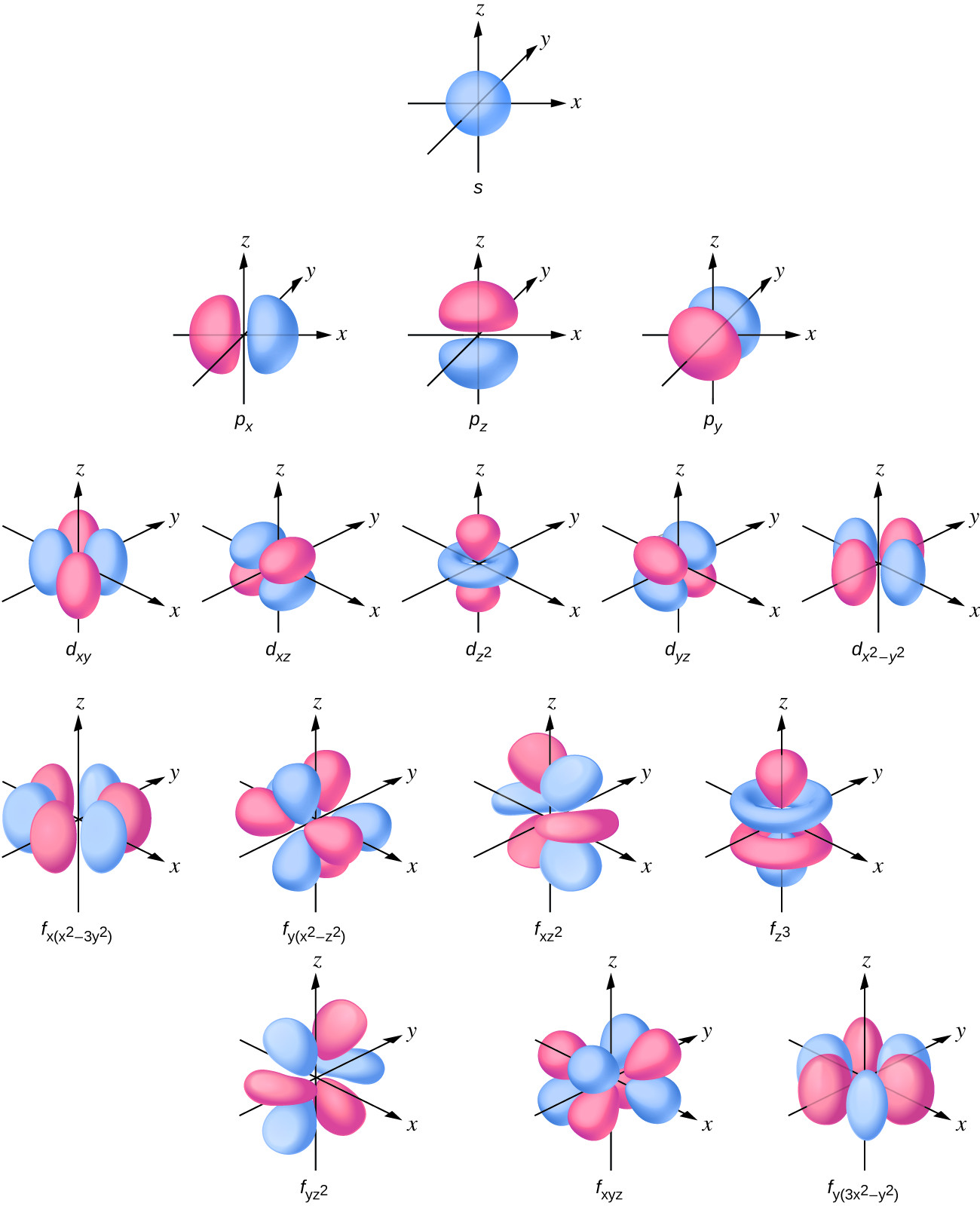
As you see, these $ Y_{l,m} $ are complex functions. For chemistry, in the literature you will rather find real valued orbitals for each subshell, that are linear combinations of these complex sub bases:
The color depicts the positive or negative regions of the orbital
For the radial component $ u_n(r) $ we get shapes of the following form with an exponential decay:
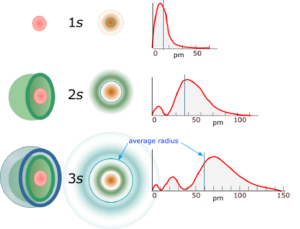
by Robert Belford – CC BY-NC-SA 4.0 via chem.libretexts.org
In general, the electron is in a superposition of many orbitals. But the electron is also coupled to the photons of the electromagnetic field. Thus, spectroscopic experiments collapse this superposition. The eigenstate with minimal energy, the groundstate, is of special importance for chemistry: Due to spontaneous emission of a photon, every excited state will relax pretty fast into the stable groundstate.
2.5 Electron-Spin in a Nutshell
It turned out, that the atomic orbitals above did not explain all spectral observations made in the early 1920s. An additional splitting of the spectral lines, representing the energy levels, was detected in the Stern-Gerlach experiment due to “some” mysterious angular momentum. In particular a doubling was observed – and this was very strange:
The splitting could only be caused by an additional angular momentum, interpreted as an intrinsic electron spin. But remember, that this all has something to do with mathematical representations of rotational symmetries. From our experience with the representations $ Y_{l,m} $, we would rather expect additional odd dimensional irreducable representations.
To explain the doubling, the Hilbert space was extended by another degree of freedom with two dimensions. Along, a two dimensional irreducable representation $S_x, S_y, S_z$ had to be constructed, that satisfies the same commutation rules as the angular components $L_i$. And this is how the Pauli matrices were discovered!
\begin{gather}
S_i = \frac{\hbar}{2} \sigma_i
\end{gather}
The discovery of the electron spin was another legendary landmark in science:
A formal reason for the electron-spin was later found. It pops up naturally in the context of relativistic quantum mechanics. The two dimensional representation of the rotational Lie algebra proved to be another mystery. The “two-component something” with a three-dimensional interpretation was named “spinor” and sparked a new branch in mathematical geometry. As the famous mathematician Sir Michael Atiyah once put it: “In some sense they describe the ‘‘square root’’ of geometry and, just as understanding the concept of $ \sqrt{−1} $ took centuries, the same might be true of spinors.” (see “A Child’s Guide to Spinors” by W. Straub for this matter i3).
Its strange orientation in space and rotational behaviour is visualized by the Bloch sphere.
The spin part of the electron’s state satisfies the following eigenequations:
\begin{align}
S^2 \lvert s, m_s \rangle &= \hbar^2 s(s+1) \lvert s, m_s \rangle \\
\text{and} \\
S_z \lvert s, m_s \rangle &= \hbar m_s \lvert s, m_s \rangle \quad \text{with} -s\le m_s \le +s
\end{align}
If you remember the diagonal form of $ \sigma_z = diag(1, -1) $, you will notice, that the spin introduces a new, half integer quantum number $m_s$ corresponding to the spin orientation $ S_z $.
The wavefunctions of the states $ \lvert u_n \rangle \otimes \lvert l, m \rangle \otimes \lvert s, m_s \rangle $ in the full Hilbert space now take the following form for spin up and spin down
\begin{gather}
u_n(r) \cdot Y_{l,m}(\theta, \varphi) \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\
u_n(r) \cdot Y_{l,m}(\theta, \varphi) \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} \\
\text{with} \\
n = 1, 2, 3, … \\
0 \le l < n \\
-l\le m \le +l
\end{gather}
These are the atomic spin-orbitals.
In quantum chemistry, you will often find the following notation for the spin-part
\begin{gather}
\alpha := \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\
\beta := \begin{pmatrix} 0 \\ 1 \end{pmatrix}
\end{gather}
Sometimes the $ \alpha $ is even omitted and only the $ \beta $ is indicated using the notation:
\begin{gather}
\psi := \psi \cdot \alpha \\
\bar{\psi} := \psi \cdot \beta
\end{gather}
2.6 Multi-electron Atoms in Quantum Chemistry
The atomic spin-orbitals of the hydrogen atom serve as an approximation even for multi-electron atoms. How are the orbitals “occupied” by the different electrons in the ground state?
The Pauli exclusion principle states, that any two electrons must differ by at least one quantum number in an atom. This forces the atoms to fill up their ground state with electrons shell by shell and subshell by subshell according to the Aufbau principle. This principle dictates the electron configuration of the ground state of each atom. The electron configuration is a multi-electron setup of orbitals: E.g. the electron configuration of the Neon atom (Ne) is
\begin{gather}
1s^2 \text{ } 2s^2 \text{ } 2p^6
\end{gather}
, meaning that the 1s, 2s, and 2p subshells are occupied by two, two, and six electrons. For a neutral atom, the total number of electrons must be equal to the charge $ Z $ of the nucleus. The electrons in the outer shell are called the valence electrons.
By Sandbh – Own work, CC BY-SA 4.0 via Wikimedia
Hund’s rules explain how the energy levels of a multi-electron atom arrange the electrons in each subshells: Each subshell is filled up with unpaired electrons and parallel spins first before each pair is completed. The parallel spins force the spatial part of the orbitals to antisymmetrize (see the reasoning below) which reduces their Coulomb-repulsion. Addionally, the atom tries to maximize its angular momentum.
3 Atomic Bonds and Molecules
3.1 Atomic Bonds
Bonding between different atoms may be grouped into the categories
- Ionic
- Metallic
- Covalent
In covalent bonding two or more atoms share electrons, creating a molecule. Two main theories explain the nature of covalent bonding:
- Valence bond theory
- Molecular orbital theory
3.2 Valence Bond Theory in a Nutshell
The Valence bond theory states, that the covalent bond is established by atomic orbitals of unpaired valence electrons (see Hund’s rule above) that constructively interfere between two atomic nuclei A and B. Thus, the nuclei are pulled together by the opposite charge of the localized electrons in the middle. There are two types of constructive interference:
Sigma bonds occur when the orbitals of two shared electrons overlap head-to-head in the inter-atomic axis.
E.g. for a $ H_2 $ molecule this may be written as
\begin{gather}
\sigma = \frac{1}{\sqrt{2}} \left( 1s_A + 1s_B \right)
\end{gather}
Pi bonds occur when two orbitals constructively overlap in parallel. Sigma bonds are stronger than pi bonds.
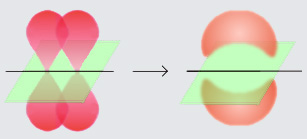
By Hati CC BY-SA 3.0 via Wikimedia
On the other hand atomic orbitals may also interfere destructively in the inter-atomic axis, resulting in excited anti-bonding orbitals $ \sigma^* $ and $ \pi^*$:
\begin{gather}
\sigma^* = \frac{1}{\sqrt{2}} \left( 1s_A – 1s_B \right)
\end{gather}
Orbital hybridisation states, that atoms establish new, mixed subshells to generate bonding hybrid-orbitals with a favorable, new degenerate energy level. For instance, the three valence electrons of Bor (see periodic table above) might form three unpaired hybrid $sp^2$-orbitals, which explains the trigonal planar geometry of $\text{BCl}_3$.
3.3 Molecular Orbital Theory
As successfull as the valence bond theory is: From a quantum mechanical standpoint the second theory for covalent bonding is more rigorous – the molecular orbital theory. It treats the molecule as a single entity with new molecular orbitals. From a quantum computing perspective, we are interested in accurate quantum mechanical calculations. And now, we start talking business …
3.4 Computational Chemistry and ab initio methods
Computational Chemistry
The main target field for quantum computing in chemistry is called computational chemistry. In the following sections, I will give you an overview and some insights into the ab initio methods in computational chemistry. These attempt to solve the eigenvalue problem of the electronic Schrödinger equation “from first principles”: As input parameters, only the positions of the nuclei and the number of electrons are used and no prior knowledge about the system is present.
Ground state energy
As I have already stated in my article “Challenging the Exponential Quantum Advantage Hypothesis for Quantum Chemistry”:
Among the various questions one can ask in quantum chemistry, probably the most central one is the question for the ground state energy of an electronic Hamiltonian. The reason for this is, that one can deduce many things from it
- If you calculate the energy for two different configurations of molecules, the difference will be the reaction energy
- If you do the same for two different phases of matter, you can study thermodynamic stability
- If you calculate the energy as a function of the nuclear coordinates, you get the potential surface for analyzing catalytic and reaction cascades
- If you study the energy in terms of externally generated perturbations you can analyze aspects of spectroscopy
Chemical Accuracy
A common goal of ab initio methods is to reach chemical accuracy while calculating energy levels of molecules, which is an error range of about $ 1 \frac{\text{kcal}}{\text{mol}} $ or $ 4 \frac{\text{kJ}}{\text{mol}} $. And just for the record, “mole” is the unit for the amount of substance and one mole contains exactly $6.022×10^{23}$ elementary entities of the substance.
An error of $ 1 \frac{\text{kcal}}{\text{mol}} $ matches the typical error found in thermochemical experiments (due to errors in temperature and mass measurements or heat loss to the surroundings). The idea is, to generate data that is as accurate as the experimentalists’ data. If the exact value is unknown one often resorts to the value of the most precise calculation possible, the Full-CI calculation. More about this later and note the difference between accuracy and precision ii.
Transition State Theory
The specific value for chemical accuracy also has some reasoning from transition state theory which analyzes the transition from reactants to product states by passing through certain intermediate states (“transition complex”) with higher energy (or higher “free energy” to be precise). This energy difference $\Delta G^+$ is the activation energy of the process.
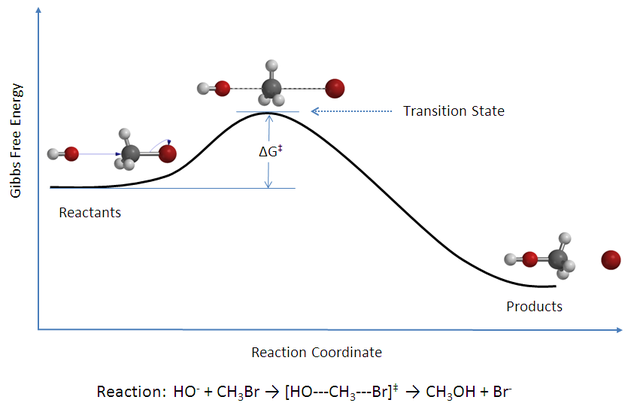
By Chem540grp1f08 – Own work, CC BY-SA 3.0, via wikimedia
TST states, that the reactants and the transition states are in a quasi-equilibrium. Its equilibrium constant $K^+$ (the quotient of their concentrations) is goverened by a thermochemical relationship ($T$ is the temperature and $k$ is a constant):
\begin{gather}
K^+ = e^{-\frac{\Delta G^+}{kT}}
\end{gather}
This relationship implies, that an accurate calculation of energy differences is crucial to compute activation rates and equilibrium constants. At room temperature this leads to the 1.36 rule: Every (additional) error of 1.36 kcal/mole for the computed energy difference results in an error of factor 10 for the equilibrium constant.
Now, how does the Schrödinger equation for a molecule look like?
3.5 The Born-Oppenheimer approximation
The general non-relativistic molecular Hamiltonian is given by
\begin{gather}
H_{\text{tot}}=
\sum_i \frac{\mathbf{p}_i^2}{2m_e} + \sum_I \frac{\mathbf{P}_I^2}{2M_I} –
\sum_{i, I} \frac{Z_I e^2}{|\mathbf{r_i} – \mathbf{R_I} |} +
\frac{1}{2} \sum_{i \neq j} \frac{e^2}{|\mathbf{r_i} – \mathbf{r_j} |} +
\frac{1}{2} \sum_{I \neq J} \frac{e^2}{|\mathbf{R_I} – \mathbf{R_J} |}
\end{gather}
Here, bold letters indicate the spatial momentum operators and spatial coordinates. Capital letters are used for the different properties of the nuclei and small letters are reserved for the electrons of the molecule. This Hamiltonian is a combination of kinetic terms of the electrons and nuclei, the electronic attraction by each electron and all nuclei and the electronic repulsion of every electron-pair and the repulsion of every nuclei-pair.
A crucial simplification of this Hamiltonian is to fix the coordinates of the nuclei and ignore their kinetic terms. This assumptions seems reasonable as the nuclei are much heavier than the electrons. To see a detailed discussion of the approximation check out the page on Wikipedia iii.
This Born-Oppenheimer approximation introduces the concept of the potential energy surface:
The Potential Energy Surface
The ground state energy changes by distorting the molecule, which means, by varying the coordinates of the nuclei: This establishes an energy landscape in the space of nuclei coordinates.
The potential energy surface enables the study of stable molecular structures (local minima) and intermediate states (saddle points) as in transition state theory. Note, that the picture of atomic (nuclear) trajectories violates the general concepts of quantum mechanics as any position is governed by the uncertainty-relationship.
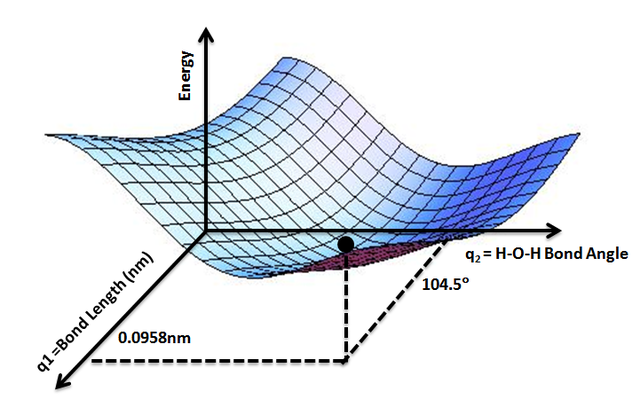
By AimNature – Own work, CC BY-SA 3.0, via Wikimedia
The Born-Oppenheimer-Hamiltonian
In the Born-Oppenheimer approximation the electronic structure problem reduces to:
\begin{gather}
H_e= \sum_i \frac{\mathbf{p}_i^2}{2m_e} – \sum_i V_{\text{nucl}}(\mathbf{r_i}) +
\frac{1}{2} \sum_{i \neq j} \frac{e^2}{|\mathbf{r_i} – \mathbf{r_j} |}
\end{gather}
To further approximate the ground state energy $E_0$ of this Hamiltonian a fundamental strategy is to use the following variatonal principle :
\begin{gather}
E_0 \leq \frac{ \langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle }{\langle \psi_{\text{trial}} \lvert \psi_{\text{trial}} \rangle}
\end{gather}
This is also the starting point of the famous Hartree-Fock method. The general idea here is, to use a trial state with a product ansatz. Unfortunately, product states have no use for identical electrons. So before we deal with the Hartree-Fock method, we need to discuss identical particles and Slater determinants.
4 The Hartree-Fock method and a Basis-Set Introduction
4.1 Slater Determinants in a Nutshell
The Slater determinant is the generic tool to generate multi-electron basis states from a set of single-electron spin-orbitals (including also non-atomic orbitals). In other words: Slater determinants are the electronic versions of product states.
One insight of quantum is, that identicals particles cannot be uniquely distinguished. The compound wave function $\psi$ must take this feature into account. Say, we have two identical particles 1 and 2 with position $\mathbf{r}_i$ and spin $s_i$. To make things easier, we use the following notation:
\begin{gather}
x_i := (\mathbf{r}_i, s_i)
\end{gather}
If we interchange the particles, their probability distribution has to stay the same. This is only possible if:
\begin{gather}
\psi(x_1, x_2) = \pm \psi(x_2, x_1)
\end{gather}
Pauli’s Spin-Statistics theorem now states, that
- Bosons: For identical particles with integer spin, the compound wavefunction is symmetric
- Fermions: For identical particles with half-integer spin, the compound wavefunction is antisymmetric
Thus, electrons are fermions. To generate a simple compound basis wave function $\psi$ from multiple electronic spin orbitals $\varphi_i$, we need to antisymmetrize it somehow. This may be done, by “simply” using the determinant of all orbitals:
\begin{align}
\psi(x_1, x_2, \dots, x_N) &= \frac{1}{\sqrt{N!}}
\begin{vmatrix}
\varphi_1(x_1) & \varphi_2(x_1) & \cdots & \varphi_N(x_1) \\
\varphi_1(x_2) & \varphi_2(x_2) & \cdots & \varphi_N(x_2) \\
\vdots & \vdots & \ddots & \vdots \\
\varphi_1(x_N) & \varphi_2(x_N) & \cdots & \varphi_N(x_N)
\end{vmatrix} \\
& = \frac{1}{\sqrt{N!}} \sum_{\sigma} \text{sign}(\sigma) \cdot \varphi_{\sigma 1}(x_1) \cdots \varphi_{\sigma N}(x_N)
\end{align}
Here, I use a simplified notation for permutations $\sigma $: $ \sigma 1 := \sigma(1) $
Often, you will find the following shorthand notation for the Slater determinant:
\begin{align}
\psi =: | \varphi_1 \varphi_2 \ldots \varphi_N |
\end{align}
As for “simply”: Note, that this term is a sum of $N!$ terms.
By the way: The determinant is zero if the $(\varphi_i)_i$ are linearly dependent. Thus, the Slater determinant is consistent with Pauli’s exclusion principle.
In particular, for two particles, we have:
\begin{gather}
\psi(x_1, x_2) = \frac{1}{\sqrt{2}} \bigl((\varphi_1(x_1) \cdot \varphi_2(x_2) – \varphi_2(x_1) \cdot \varphi_1(x_2) \bigr)
\end{gather}
4.2 The Hartree-Fock method in Quantum Chemistry
Now let’s get into the most basic ab initio method: The Hartree-Fock method. Besides being a low order approximation of the real molecule, it also generates a set of canonical molecular orbitals which form the basis for the higher order methods!
Varying the Slater determinant
The idea is, to find the best set of spin orbitals, whose Slater determinant minimizes the variational principle above. This will generate us a new eigenequation. The solutions of this equation will give us the canonical molecular orbitals. We will try to keep our notation for the $x_i$ as long as possible:
\begin{align}
\langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle & =
\frac{1}{N!} \sum_{\nu, \mu} \text{sign}(\nu) \cdot \text{sign}(\mu) \int dx_1 \cdots dx_n \cdot \varphi^*_{\nu 1}(x_1) \cdots \varphi^*_{\nu N}(x_N) \\
& \bigr( \sum_i \frac{\mathbf{p}_i^2}{2m_e} – \sum_i V_{\text{nucl}}(\mathbf{r_i}) +
\frac{1}{2} \sum_{i \neq j} \frac{e^2}{|\mathbf{r_i} – \mathbf{r_j} |}
\bigl) \cdot \varphi_{\mu 1}(x_1) \cdots \varphi_{\mu N}(x_N)
\end{align}
To formally vary this equation via $ \delta / \delta \varphi^*_k(x) $ we have to consider, that we are only interested in orthonormal spin-orbitals (note the fixed index $k$ as there are several indices present). We take this constraint into account by introducing Lagrange multipliers $ \epsilon_{ij} $:
\begin{align}
\delta E_0[\varphi^*_k] = \delta \langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle – \delta \bigl( \sum_{i,j} \epsilon_{ij}
\cdot (\langle \varphi_i \lvert \varphi_j \rangle – \delta_{i,j})
\bigr) \stackrel{!}{=} 0
\end{align}
As we are free to rotate our spin-orbitals via unitary transfomations, we may simplify the Lagrange multipliers to
\begin{gather}
\epsilon_{ij} = \epsilon_i \cdot \delta_{i,j}
\end{gather}
The expectation value $\langle \psi \lvert H_e \lvert \psi \rangle $ is not as bad as it looks. It contains only one-electron contributions and two-electron contributions. We may resolve all permutations and their sums by symmetry arguments of these contributions. You will find the detailed derivation and some online sources for it in the
Appendix 1: Derivation of the Hartree-Fock equations and the Fock operator
This leads to the to the Hartree-Fock equations:
Hartree-Fock equations
\begin{gather}
\bigr( \frac{\mathbf{p}^2}{2m_e} – V_{\text{nucl}}(\mathbf{r})
+ \sum_{j \neq k} \int dx’ \cdot \frac{e^2}{|\mathbf{r} – \mathbf{r’} |} \varphi^*_j(x’) \cdot \varphi_j(x’) \bigl) \varphi_k(x) \\
– \sum_{j \neq k} \int dx’ \cdot \frac{e^2}{|\mathbf{r} – \mathbf{r’} |} \varphi^*_j(x’) \varphi_j(x) \frac{\varphi_k(x’)}{\varphi_k(x)} \cdot \varphi_k(x) = \epsilon_k \varphi_k(x)
\end{gather}
The first two-electron term may be interpreted as a Coulomb repulsion of an electron $k$ at the position $ \mathbf{r} $ due to the presence of all the other electrons.
The second two-electron term is due to the Pauli exclusion principle as shown in the appendix 1. It is called the exchange potential. Unfortunately it is a non-local term, as the spin-orbital $ \varphi_k (x’) $ is part of the integration kernel over $x’$. For now, we ignore this problem and deal with it later.
Now it’s time to resolve our notational convention:
\begin{gather}
x := (\mathbf{r}, s) \text{ and } x’ := (\mathbf{r’}, s’) \\
\int dx’ := \sum_{s’} \int d^3 r’
\end{gather}
and also take into account, that summation indices and the spin orbitals factor in a spatial and a spin part
\begin{gather}
j := (\mathbf{j}, \alpha) \text{ and } k := (\mathbf{k}, \beta) \\
\varphi_j(x) := \varphi_\mathbf{j}(\mathbf{r}) \cdot \sigma_\alpha(s)
\end{gather}
As demonstrated in the appendix 1: The integration of the term for the Coulomb potential and its sum of the spins is straight forward.
For the exchange potential we have to integrate $\varphi^{*}_j(x’) \cdot \varphi_k(x’) $ over $x’$. This time, we have to closely pay attention to the integrals over the spin-part: Only those terms of $\varphi^{*}_j$ contribute, that are polarized with spins parallel to $\varphi_k$.
The resulting eigenequation may be written in a compact form:
\begin{gather}
F \varphi_k = \epsilon_k \varphi_k \\
\text{with} \\
F = \sum_i^{\text{occ}} \bigl( \frac{\mathbf{p}_i^2}{2m_e} – V_{\text{nucl}}(\mathbf{r_i}) \bigr) +
\sum_i^{\text{occ}} \bigl( 2 J_i – K^{polar}_i\bigr)
\end{gather}
$F$ is called the Fock operator. Note, that by now we are left dealing only with occupied spatial orbitals and their spatial indices.
4.3 The Self-Consistent Field Method
Now, the Hartree-Fock equation contains these non-local terms. This means, to construct the Fock operator we need to know the complete spin-orbitals in the first place. But we need to know the operator in order to find the orbitals. To deal with this chicken-and-egg problem, one uses on iterative approach:
- 1. Take a good educational guess for an initial set of orbitals $\varphi_k^{(0)}$.
- 2. Using these functions, we construct $J_k^{(0)}$, $K_k^{(0)}$ and $F^{(0)}$
- 3. We solve the Hartree-Fock equation and obtain orbital energies $\epsilon_k^{(1)}$ and new orbitals $\varphi_k^{(1)}$
- 4. Using these new functions, we construct $J_k^{(1)}$, $K_k^{(1)}$ and $F^{(1)}$
We keep on going until we reach an iteration step $n$ with $ F^{(n)} = F^{(n-1)} $. Thus, we have hit a fix point. Because of this self-consistency strategy, the Hartree-Fock method is also called the self-consistent field (SCF) method.
As pointed out above, in general there is a spin inconsistency in the Hartree-Fock equation: Starting from an initial spin-orbital the $\alpha$ part and the $\beta$ part of the orbital develop differently throughout the iteration. E.g. consider a HF-calculation for the Lithium atom $1s^2 2s^1$: There, we have two $\alpha$ contributions for the exchange potential ($1s\alpha$ and $2s\alpha$) but only one $\beta$ contribution ($1s\beta$). One consequence of this spin-polarized potential is, that a $\varphi_k\alpha$ and a $\varphi_k\beta$ orbital develop a different spatial form.
But the Hamiltonian of the Born-Oppenheimer approximation commutes with the spin operator and any reasonable spin-orbital should be a product state of spatial orbital and its spin-part. To fix this problem we consider only closed shell problems with equal spin contributations and a restricted Hartree-Fock (RHF) method. Fortunately, many interesting situations are closed shell. There are also unrestricted Hartree-Fock methods (UHF) out there which is beyond the scope of this article. See chapter 18 in “Quantum Mechanics in Chemistry” by Simons and Nichols for details iv.
Electron correlations
Above we saw, that in the Hartree-Fock approximation, each electron experiences a Coulomb-repulsion of a fixed electron-cloud and all individual interactions are integrated out. This makes the Hartree-Fock approximation a mean field approximation. The energetical error of the Hartree-Fock method is called the correlation energy.
\begin{gather}
E_\text{correlation} = E_\text{true} – E_\text{Hartree-Fock}
\end{gather}
Due to the exchange potential, the Hartree-Fock approximation also does contain a correlation, but this Fermi-correlation is of generic type and all Coulomb-correlations are neglected.
Since the true ground state is lower than the HF-state, the correlation energy is always negative. There are different contributions to the correlation energy:
- dynamical correlation is due to the individual repulsion between each pair of electrons
- static correlation is due to the fact, that the HF-method is based on a single Slater determinant
4.4 The Roothaan-Hall SCF in a Nutshell
The Hartree-Fock equations are 3 dimensional integro-differential equations. Although they were found in the early 1930ths, for a long time numerical calculations could only be performed for atoms. It took another 20 years to make them feasible for molecular calculations. The main idea is to expand the Hartree-Fock orbitals into a set of $M$ atom centered basis functions $\chi_j$.
\begin{gather}
\varphi_i = \sum_{j=1}^M c_{ij} \cdot \chi_j
\end{gather}
This set may not be orthonormal. The approach turns the Hartree-Fock equations into a linear algebraic problem containing a Fock-matrix $F_{ij}$ and an overlap-matrix $S_{ij}$
\begin{gather}
F \cdot c_i = \epsilon_i \cdot S \cdot c_i
\end{gather}
With
\begin{gather}
S_{ij} = \int d^3 r \cdot \chi^*_i (\mathbf{r}) \chi_j (\mathbf{r})
\\
\text{and}\\
F_{ij} = \int d^3 r \cdot \chi^*_i (\mathbf{r}) F \chi_j (\mathbf{r})
\end{gather}
Altogehter these are $ \frac{M^2}{2} $ one electron integrals and $ \frac{M^4}{8} $ two electron integrals. Like any matrix-eigenequation this is first solved by finding the roots of the characteristic polynom (in $\epsilon$) via the secular equation:
\begin{gather}
| F – \epsilon \cdot S | = 0
\end{gather}
This will give us all Fock-energy levels $ \epsilon_i $. Next, the eigenvectors of each eigenvalue are resolved using standard methods in linear algebra. Altogether, there will be $M$ eigenvectors, so the size of the basis set dictates the number of molecular orbitals.
You can imagine: The success of this method crucially depends on the selected basis set.
4.5 Gaussian type basis sets STO-nG
At first, Slater type orbitals (“STO”) where used: Simplified atomic orbitals with an exponential decay. This ansatz is also called linear combination of atomic orbitals LCAO. But these basis sets were difficult to handle. Much more convenient was the ansatz to approximate each single Slater type orbital using a superposition of $n$ primitive Gaussian type (“G”) functions with an quadratic exponential decay. The fixed coefficients of each superposition (“contraction”) are optimized by the community and may be looked up in databases for reuse.
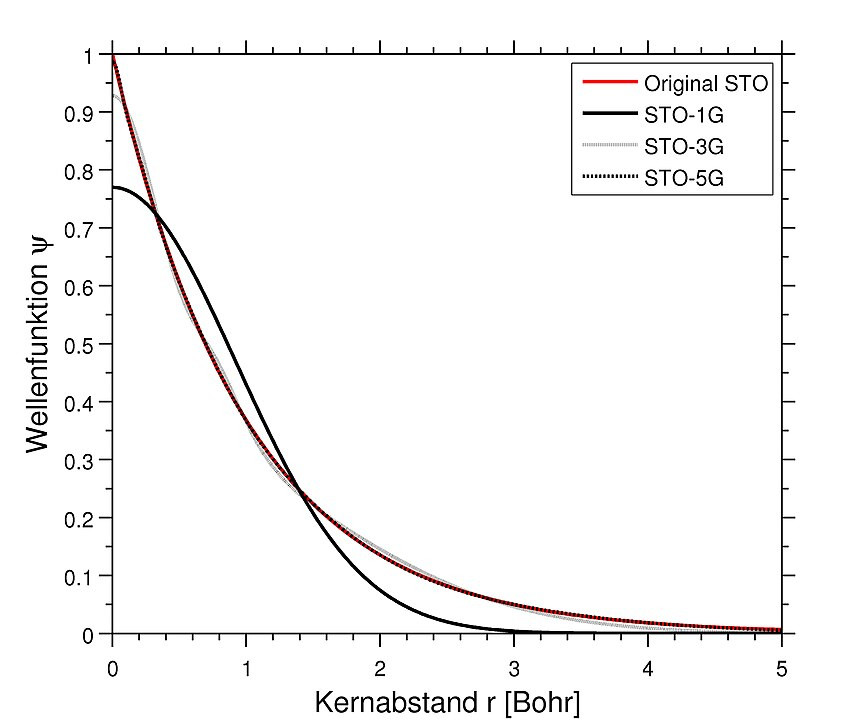
Credits Jannick88 – own work, CC BY-SA 3.0
The main benefit of using Gaussian type functions is, that products of two Gaussians are again a Gaussian function and integrals may be expressed in an analytic form.
A minimal basis set is a set, with a single contracted basis function for each electron. Yet, there might be cases, for which this proves to be insufficient for describing a certain molecular orbital. For example, the sigma-bond of a H-H molecule looks very different from a sigma-bond of H-F molecule.
To add flexibility, the multiple zeta concept was introduced, which uses multiple basis functions for a certain or several electrons. Here, the “zeta” refers to the exponent of a STO basis function. This is also called “decontraction” because instead of fixing the coefficient, you start to vary it, as the other variables:
For instance the split valence variant of the STO-nG sets uses the naming scheme
“X-YZG”.
example “3-21G”:
- “3”: Each orbital of core electrons (non-valence) is approximated using 1 basis function with 3 primitive Gaussian functions
- “21” (length 2): The split-level of the basis set. Each valence electron is represented by 2 basis functions. These may be centered differently, resulting in a vaulted or stretched superposition
-
- “2.”: The first basis function is approximated using 2 primitive Gaussian functions
- “.1”: The second basis function is approximated using 1 primitive Gaussian functions
For example the STO-3-21G basis set for the $\text{NH}_3$ molecule requires 15 basis functions with altogether 24 primitives v.
You can further enhance this basis set by adapting to polarization features of the molecule: For instance a fixed number of p-functions are added to every H-atom. These polarization functions possess a higher angular momentum, than the electron you want to represent. They are able to push the electron orbitals of an atom into the direction of polarization. E.g. this is the case in the water molecule $H_2O$, where the O-atom pulls the electrons away from the H-atoms.
4.6 Dunning’s Correlation Consistent Basis Sets cc-pVnZ
The idea to approximate real atomic orbitals by Gaussian functions proved to be very successful. In the late 1980s two programs started, to enhance these basis sets. The central guiding questions were:
- Is it possible to optimize a contraction not according to their shape but according to their actual purpose – to decrease the correlation energy?
- Is it possible to improve this systematically?
The first question was answered positively by the Atomic Natural Orbital Basis Sets (ANO). Here, the contraction coefficients of the Gaussian primitives were directly calculated using Post-Hartree-Fock methods like Full CI (more about these terms later).
The second question was answered positively by a striking observation made by Dunning and co-workers vi:
It is possible to incrementally group additional polarization basis functions consistently according to their contributions to the correlation energy. For example for the oxygen atom:
- group 1: Adding a 1st 2d-function has by far the largest effect on the correlation energy
- group 2: Adding a 2nd 2d-function has approximately the same effect as adding a 1st 2f-function
- group 3: Adding a 3rd d-function, a 2nd f-function and 1st g-function all have the same effect
- … and so on
By combining these polarization groupings with Gaussian split-valence groups of double zeta, triple zeta and quadruple zeta quality, the basis sets cc-pVDZ, cc-pVTZ … cc-pVnZ were derived: The correlation consistent polarized valence n zeta sets. Besides providing a systematically improving framework, the correlation consistent basis sets significantly reduced the amount of primitive functions compared to the ANO sets. Up to today, these features make them a tool of choice for high-accuracy calculations in quantum chemistry and chemical calculations in quantum computing.
The correlation consistent basis sets were first constructed for the first row elements, later for all second and third row elements. Throughout the years the correlation consistent framework was further improved in various ways:
By including correlations of core electrons cc-pCVnZ and relativistic effects cc-pVnZ-DK . Correlation consistent basis sets with an aug--prefix are augmented with extra “diffuse” functions (functions small exponents), to support excited states and systems where long-range interactions are significant and other applications. You may find a very readable introduction “Gaussian basis sets for molecular applications” by J. Grant vii, who is one of the contributors to the program and also runs the website “ccRepo” viii.
To give you an idea of the amount of contracted Gaussian primitives to the amount of basis functions here is an overview of the DZ-, TZ- and QZ-granularity for H-He and B-Ne:
- cc-pVDZ gives: H (4s,1p / 2s,1p), B-Ne (9s,4p,1d / 3s,2p,1d)
- “(4s,1p / 2s,1p)” means: 4s-type pimitives contracted to produce 2s basis functions and 1p-type primitive contracted to produce 1p basis function
- cc-pVTZ gives: H (5s2p1d / 3s2p1d), B-Ne 10s5p2d1f / 4s3p2d1f)
- cc-pVQZ gives: H (6s3p1d1f / 4s3p2d1f), B-Ne (12s6p3d2f1g / 5s4p3d2f1g)
Note, that it is useful to reuse a certain Gaussian primitive in the contraction of several basis functions as their integrals only need to be computed once. See “Quantum Mechanics in Chemistry” chapter 18 for details ix.
The Gaussian-type basis functions boost the calculations of the different methods in quantum chemistry. But still, the evaluation of integrals and the transformation from the atomic basis into the molecular basis become more and more dominating with the growing system size. To solve this problem, the approximation strategy density fitting has been established x.
4.7 Computer aided Quantum Chemistry
All of this appears to be extremely complex and real calculations must be extremely time consuming. In fact, they are not. There are numerous modern and very smart software libraries that abstract away many of the gory details of these calculations and support even very advanced methods. For example, calculating the restricted Hartree-Fock-solution of a water molecule using the popular Python-framework PySCF may be as simple as this:
mol_h2o = gto.M(atom = 'O 0 0 0; H 0 1 0; H 0 0 1',
basis = 'ccpvdz')
rhf_h2o = scf.RHF(mol_h2o)
e_h2o = rhf_h2o.kernel()
5 Post-Hartree-Fock I: From Configuration Interaction to Multireference
5.1 About the error of the Hartree-Fock method
An important question, that we should ask ourself is: What is the accuracy of the Hartree-Fock method?
Let’s consider the He-atom: The following shows a comparison of the Hartree-Fock ground state energy and the exact energy obtained from experiments:
\begin{gather}
E_\text{HF} = -2.861 68 \text{ hartrees}
\\
E_\text{exact} = -2.903 72 \text{ hartrees}
\end{gather}
Here, we used another energy unit hartree or atomic unit which is about $ 1 \text{ hartree} = 627.5 \text{ kcal/mol} $ xi.
This is a relative error of 2% which looks actually pretty good. But only at first sight: The absolute error is about $ 26 \text{ kcal/mol} $. If you remember the 1.36 rule from above, you will see that this results in a factor of almost $10^{20}$ in terms of the equilibrium constant or rate constant xii!
And this is due to only one additional electron compared to the H-atom which has an exact Hartree-Fock solutions.
We see, that the Hartree-Fock method gives a good approximation for the ground state energy. But in terms of chemical accuracy we need better tools: We need Post-Hartree-Fock methods. From a quantum computing perspective we could argue: The electron correlations introduce a series of controlled operations. So, there is no way, that a single Slater determinant is able to catch all of the molecule’s entanglement. The following example illustrates this futher:
According to the Aufbau-principle, the Hartree-Fock solution of the Be-atom has the configuration
\begin{gather}
\psi_\text{Be, HF} = |1s\alpha, 1s\beta, 2s\alpha, 2s\beta|
\end{gather}
The exact ground state is better approximated by a superposition of the type xiii
\begin{gather}
\psi_\text{Be, exact} = C_1 \cdot \psi_\text{Be, HF} + C_2 \cdot
|1s^2, 2p^2| \\
\\
\text{whereas the second term is a abreviation for} \\
|1s^2, 2p^2| := \\
∣1sα, 1sβ, 2p_0α, 2p_0β∣ – ∣1sα, 1sβ, 2p_1α, 2p_{−1}β ∣ – ∣1sα, 1sβ, 2p_{−1}α, 2p_1β∣
\end{gather}
The two constants have a ratio of about 90% to 10% .
There are several ways to systematically improve the Hartree-Fock solution and the following sections deal with these methods.
First of all, we note that the variational principle proved to be a very powerful tool. Can we exploit this even further?
5.2 Full Configuration Interaction FCI in a Nutshell
Note, that every wavefunction may be expressed by a basis of product states. Likewise, any wavefunction may be expressed as a superposition of many-electron Slater determinants as long as their single-electron orbitals form a complete basis of the one-electron Hilbert space.
The CI-basis
The Hartree-Fock-solutions form such a complete basis in a canonical way. It contains the occupied orbitals: the orbitals, that are actually occupied by the electrons in the HF-ground state. Also it contains excited states, called virtual orbitals, not occupied by the ground state. A systematic way to desribe this, is
- to first consider all Slater determinants of one-electron-excitations to all possible virtual orbitals
- then consider all Slater determinants of two-electron-excitations,
- all three-electron-excitations, …
- of the occupied orbitals $i, j, k, …$ to all possible virtual orbitals $a, b, c, … $ and so on.
We write this as:
\begin{gather}
\Phi_{HF} = |\varphi_1, \varphi_2, \varphi_3, \ldots | \\
\Phi_i^a = |\varphi_1, \varphi_2, \ldots, \varphi_{i-1}, \varphi_{a}, \varphi_{i+1}, \ldots | \\
\Phi_{ij}^{ab} = |\ldots, \varphi_{i-1}, \varphi_{a}, \varphi_{i+1}, \ldots, \varphi_{j-1}, \varphi_{b}, \varphi_{j+1}, \ldots | \\
\Phi_{ijk}^{abc} = |\ldots, \varphi_{a}, \ldots, \varphi_{b}, \ldots, \varphi_{c}, \ldots |
\end{gather}
This gives:
\begin{gather}
\Psi = c_0 \cdot \Phi_{HF} + \sum_{i,a} c_{ia} \cdot \Phi_i^a + \sum_{ij, ab} c_{ijab} \cdot \Phi_{ij}^{ab} + \sum_{ijk, abc} c_{ijkabc} \cdot \Phi_{ijk}^{abc} + \cdots
\end{gather}
Expanding $\Psi$ into all possible molecular orbital configurations like this, gives us a full configuration expansion.
For notational convenience we just write:
\begin{gather}
\Psi = \sum_I c_{I} \cdot \Phi_I
\end{gather}
Although the equality is exact, we have to keep in mind, that for practical calculations, we need to choose a proper basis set which introduces a certain error depending on the quality of the basis functions. As I have mentioned above, the size of the basis set dictates the number of orbitals. While the number of occupied orbitals will stay constant, a better basis will introduce more virtual orbitals $a, b, c, \ldots$ and thus increase the configuration-expansion in the FCI-calculation.
The CI-matrix
Starting from the above expansion, we again use the variational principle. This time, the molecular oribitals are fixed and we have to vary the CI-coefficients $ c_I $. As the $ \Psi $ is linear in these coefficients, the variation gives a very simple secular form xiv:
\begin{gather}
\sum_J \left(H_{IJ} – E \cdot S_{IJ} \right) \cdot c_I = 0
\text{ for all $I$}
\end{gather}
Whereas
\begin{gather}
H_{IJ} = \langle \Phi_I \lvert H \lvert \Phi_J \rangle
\quad \text{and} \quad
S_{IJ} = \langle \Phi_I \lvert \Phi_J \rangle
\end{gather}
In part II of this series we will derive the matrix $ H_{IJ} $ much more explicitely. For now we emphasize, that in the CI-basis the Hamiltonian-matrix has the following structure:
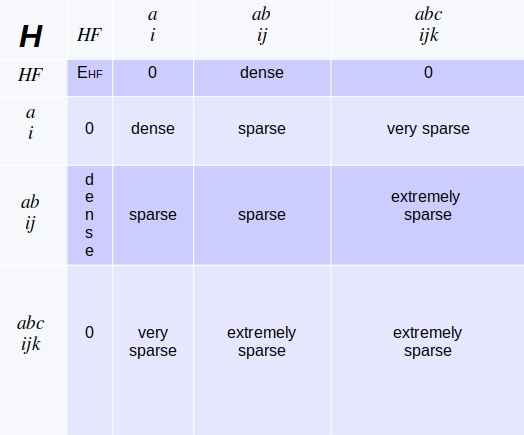
Redrawn from, https://www.youtube.com/watch?v=5BZxa6fZHZU&list=PLkNVwyLvX_TFBLHCvApmvafqqQUHb6JwF&index=19
Two theorems provide an insight, how the Hamiltonian matrix $ H_{IJ} $ looks like: Brillouin’s theorem states, that the matrix-elements for the Hartree-Fock determinant and single excited determinants are zero. The Slater-Condon rules outline a systematic way to analyze the matrix-element $O_{IJ}$ of two Slater determinants $\Phi_I, \Phi_J$ on one- and two-body operators, if these determinants are
- a) the same
- b) differ by only one orbital and
- c) differ by two orbitals
You got an impression of these rules in our derivation of the Fock-operator.
One collary of these rules is, that the matrix-elements of the Hamiltonian is zero for elements that are more than two blocks off-diagonal. Again, we will get a more detailed look at how these matrix elements look like using the framework of second quantization in the context of the MCSCF method.
Full CI: Computational limits
As indicated by the picture above, the subspaces are getting extremely large, if we include more and more excitations due to a their $\left( ^n_k \right) $-type of size. Also note, that we express the molecular orbitals in the Slater determinants as vectors of the chosen basis set. Thus, each block increases in size if we increase the quality of the set.
For these reasons, full configuration interactions can be carried out only for small systems. For instance: A recent example for the $C_3H_8$-molecule and the STO-3G basis set used 1.31 trillion determinants xv. The Full CI calculation was heavily distributed among 256 servers. A goal for such computations is to compare the accuracy of various Post-Hartree-Fock-methods including quantum chemical computations.
5.3 Configuration State Functions CSF in Quantum Chemistry
If you remember the exact form of the Born-Oppenheimer approximation you will notice, that the Hamiltonian does not depend on the electrons’ spins. Thus, the true ground state of the system should be an eigenstate of the spin and maybe other operators / symmetries.
In general the CI-determinants might not qualify for these properties. To fix this issue, in practise we construct a superposition of configurations which are adapted for these symmetries. Note, that these configuration state functions (CSF) are contracted functions with fixed coefficients. Thus, in all our equations we have to keep in mind, that the configurations $\Phi_J$ could be Slater determinants or configuration state functions.
To illustrate the point above, I follow a nice and simple example by Nikita Matsunaga xvi:
We may express a general two-electron system $a, b$ with $(\phi \alpha, \psi \beta)$ in the following basis, which is an eigenbasis of the total spin $ \mathbf{S}^2 = \left( \mathbf{S}^\text{(a)} + \mathbf{S}^\text{(b)} \right)^2 $ and its total z-component $ S_z = S_z^\text{(a)} + S_z^\text{(b)} $:
\begin{align}
S_1 := & \left( \phi \psi + \psi \phi \right) /\sqrt{2} \cdot \left( \alpha \beta – \beta \alpha \right)/\sqrt{2} & \text{ “$S_1$” for “singlet” with $2S+1 = \mathbf{1}$} \\
\\
T_1 := & \left( \phi \psi – \psi \phi \right)/\sqrt{2} \cdot \alpha \alpha & \text{ “$T_i$” for “triplet” with $2S+1 = \mathbf{3}$} \\
T_2 := & \left( \phi \psi – \psi \phi \right)/\sqrt{2} \cdot \left( \alpha \beta + \beta \alpha \right)/\sqrt{2} \\
T_3 := & \left( \phi \psi – \psi\phi \right)/\sqrt{2} \cdot \beta \beta
\end{align}
On contrary, the following generic Slater determinants are not eigenstates of the total spin $S^2$:
\begin{align}
D_1 := & |\phi \alpha, \psi \beta | \\
D_2 := & |\psi \alpha, \phi \beta |
\end{align}
You will see this, if you expand $D_1$ and $D_2$ in the singlet and triplet basis
\begin{align}
S_1 = & \left( D_1 + D_2 \right) / \sqrt{2} \quad \quad \text{or}
& D_1 = & \left( S_1 + T_2 \right) / \sqrt{2} \\
T_1 = & \left( D_1 – D_2 \right) / \sqrt{2} \quad \quad
& D_2 = & \left( S_1 – T_2 \right) / \sqrt{2}
\end{align}
Thus, $D_1$ and $D_2$ are a mix of a singlet state and a triplet state : They are spin contaminated. To fix this, we have to consider the superpositions of both determinants on the left. You will also find a detailed discussion of configuration state functions in chapter 10 in “Quantum Mechanics in Chemistry” by Simons and Nichols xvii.
Luckily, the construction of the configuration state functions is a technical issue, that the software libraries will take care for you! Very nice …
5.4 Truncated Configuration Interaction CISD, CISDT, … and size inconsistency
For the purpose of the Full Configuration Interaction we don’t necessarily have to rely on the Hartree-Fock determinant as a reference state $\Phi_0$. But the Hartree-Fock orbitals and their excitations present an obvious strategy on how to improve the result or how to reduce the complexity of the calculation: We should expect that single excitation of the Hartree-Fock approximation will contribute the most to the correction for the true groundstate, then double excitations, …
If we restrict our expansion, say to single and double excitations or single, double and triple excitations, this should significantly speed up the calculation. This is called Truncated Configuration Interaction e.g. CISD, CISDT, CISDTQ, …. Note, that truncating to single excitations would not work, because of Brillouin’s theorem: The Hamiltonian-matrix is block diagonal in the truncated basis $(\Phi_{HF}, \Phi_i^a)$, so there would not be any mixing of the two subspaces.
Yet, truncated configuration interaction has a serious flaw:
Consider two $H_2$-molecules far away from each other so there is no interaction between them. The ground state energy $E_{2H_2}$ of this “system” will be twice the ground state energy of a single $H_2$-molecule:
\begin{gather}
E_{2H_2} = 2 \cdot E_{H_2}
\end{gather}
Due to Brillouin’s theorem, we may calculate $ E_{H_2} $ of a single molecule using a truncated configuration interaction with single and double excitations. Yet, to calculate the ground state energy of the two molecules we would also have to consider triple and quadruple excitations as the compound orbitals are just outer products of two individual orbitals.
This shows, that the truncation introduces a systematic error in certain cases. The problem is called size inconsistency and is a reason, why other Post-Hartree-Fock-methods are preferred. More about those later.
5.5 Single-Reference and Multi-Reference systems in Quantum Chemistry
In the configuration interaction methods above we have assumed, that it is a good idea, to base our expansion-method on a single determinant. Systems for which this is the case are called single-reference systems .
Yet, the assumption, that a single determinant approximates a molecular orbital well, breaks down in several cases. Namely for xviii:
- Diradicals
- Excited states
- Transition states (like bond breaking)
- Unsaturated transition metals
- High energy species
- Generally, any system with near degeneracies
Such systems are called multi-reference systems . Thus, systems with a strong multi-reference character show strong static correlations (note our definition for correlation types from above).
Let’s illustrate this a little bit: Recall, that the canonical orbitals have been optimized for the ground state energy during the Hartree-Fock calculation. Besides the occupied orbitals, the solution also gave us a bunch of virtual orbitals. But we shouldn’t expect, that these are good approximations for the actual excited states: The occupied orbitals were explicitely included and iteratively improved throughout our self consistent field method, while the virtual orbitals are just implicite solutions.
Also, it is obvious, that systems with degeneracies or near degeneracies will probably not be described well by a just single determinant: We will have to decide, which of the two degenerate orbitals (or more) should be used in our trial determinant. Only this orbital will be improved throughout our self consistent field optimization, whereas there is another orbital that should be considered just as well. If we had a way to improve both orbitals at the same time, we should expect that the resulting molecular orbitals are much closer to the actual physical system.
Fortunately, there is a cure for this – but a very expensive one …
5.6 The Multiconfiguration Self Consistent Field method MCSCF I
The cure is called Multiconfiguration Self Consistent Field method MCSCF. Practically it is a two-fold optimization procedure:
We start with a full or truncated configuration interaction. We include all configurations of only those trial orbitals, that we find most relevant for the superposition of the ground state of the particular system.
This time, we explicitly include excited orbitals using different configurations. Also we consider all degenerate orbitals.
- In the outer optimization loop, we optimize the CI-coefficients like explained above. After we have calculated these coefficients, we start …
- … The inner optimization loop: We fix the CI-coefficients and vary the molecular orbitals (which we had fixed before) using a self consistent field method. Now we have a set of improved molecular orbitals.
- Then we start the next iteration: We continue with the outer loop and do another CI-optimization, using the fixed and improved configurations. We obtain a new set of CI-coefficients, that we fix to continue with the inner loop: Another variation of the molecular orbitals.
- … We keep on going until our method converges.
All in all these are lots of lots of terms and optimization variables. The fact, that it took us quite some effort to derive the molecular orbital equations for just a single CI-function, the Hartree-Fock Slater determinant, should make look it pretty hopeless to find a set of MO-equations for a family of arbitary CI-functions.
Yet, it is very remarkable, that this may actually be expressed in closed forms. It is the broad generalization of the Hartree-Fock and the Full CI-equation. But before we get into the details of the multiconfiguration self consistent field method we have to master another technical tool, just like we have mastered Slater determinants earlier. It is a fundamental ground work for all quantum field theories. More important for us: It sets the stage for quantum computing algorithms in quantum chemistry.
This is all part of my:
5.7 My follow-up article: More about Post-Hartree-Fock methods
This finishes my introduction to the basic concepts in traditional quantum chemistry. As promised we get deeper into Second Quantization, MCSCF-and other Post-Hartree-Fock methods in my second article. For these methods we will outline to following aspects:
- What are their underlying concepts?
- How do their fundamental equations actually look like?
- How are they solved?
- What is their scaling?
- Some cutting-edge examples, that have been carried out
To be specific part II deals with the following topics:
Article / Part II: More about Post-Hartree-Fock methods
- Introduction to Second Quantization
- A detour to Quantum computing for chemistry: About the Jordan-Wigner transformation, the Aspuru-Guzik / Whitfield-method and a roadblock for VQE
- Multireference, the MCSCF- and CASSCF-methods and optimizing molecular orbitals
- Coupled Cluster theory and Coupled Cluster Pertubation theory
- Møller-Plesset perturbation theory
- CCSD(T): The “gold standard” of quantum chemistry and some concrete equations for its 4th and 5th order corrections
- DMRG, exploiting quasi 1-dimensional systems
See you there 🙂
6 Appendix 1: Derivation of the Hartree-Fock equations and the Fock operator
To generate a simple compound basis wave function $\psi$ from multiple electronic spin orbitals $\varphi_i$, we need to antisymmetrize it somehow. This may be done, by using the determinant of all orbitals:
\begin{align}
\psi(x_1, x_2, \dots, x_N) &= \frac{1}{\sqrt{N!}}
\begin{vmatrix}
\varphi_1(x_1) & \varphi_2(x_1) & \cdots & \varphi_N(x_1) \\
\varphi_1(x_2) & \varphi_2(x_2) & \cdots & \varphi_N(x_2) \\
\vdots & \vdots & \ddots & \vdots \\
\varphi_1(x_N) & \varphi_2(x_N) & \cdots & \varphi_N(x_N)
\end{vmatrix} \\
& = \frac{1}{\sqrt{N!}} \sum_{\sigma} \text{sign}(\sigma) \cdot \varphi_{\sigma 1}(x_1) \cdots \varphi_{\sigma N}(x_N)
\end{align}
Here, I use a simplified notation for permutations $\sigma $: $ \sigma 1 := \sigma(1) $
As for “simply”: Note, that this term is a sum of $N!$ terms.
The Hartree-Fock method
The idea is, to find the best set of spin orbitals, whose Slater determinant minimizes the variational principle above. This will generate us a new eigenequation. The solutions of this equation will give us the canonical molecular orbitals. We will try to keep our notation for the $x_i$ as long as possible:
\begin{align}
\langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle & =
\frac{1}{N!} \sum_{\nu, \mu} \text{sign}(\nu) \cdot \text{sign}(\mu) \int dx_1 \cdots dx_n \cdot \varphi^*_{\nu 1}(x_1) \cdots \varphi^*_{\nu N}(x_N) \\
& \bigr( \sum_i \frac{\mathbf{p}_i^2}{2m_e} – \sum_i V_{\text{nucl}}(\mathbf{r_i}) +
\frac{1}{2} \sum_{i \neq j} \frac{e^2}{|\mathbf{r_i} – \mathbf{r_j} |}
\bigl) \cdot \varphi_{\mu 1}(x_1) \cdots \varphi_{\mu N}(x_N)
\end{align}
To formally vary this equation via $ \delta / \delta \varphi^*_k(x) $ we have to consider, that we are only interested in orthonormal spin-orbitals (note the fixed index $k$ as there are several indices present). We take this constraint into account by introducing Lagrange multipliers $ \epsilon_{ij} $:
\begin{align}
\delta E_0[\varphi^*_k] = \delta \langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle – \delta \bigl( \sum_{i,j} \epsilon_{ij}
\cdot (\langle \varphi_i \lvert \varphi_j \rangle – \delta_{i,j})
\bigr) \stackrel{!}{=} 0
\end{align}
As we are free to rotate our spin-orbitals via unitary transfomations, we may simplify the Lagrange multipliers to
\begin{gather}
\epsilon_{ij} = \epsilon_i \cdot \delta_{i,j}
\end{gather}
The expectation value $\langle \psi \lvert H_e \lvert \psi \rangle $ is not as bad as it looks. It contains only one-electron contributions and two-electron contributions. The orbitals of the other electrons are not touched by the operators, so we may simplify the calculation xix:
One-particle contribution
The integrals of the untouched orbitals $ \int dx_n \varphi^*_{\nu n}(x_n) \varphi_{\mu n}(x_n) $ is equal to $ \delta_{\nu n,\mu n} $ for all $n$ which gives $ \delta_{\nu, \mu} $ altogether. This takes care of one sum over permutations. The other sum over permutations gives $N!$ terms, which permute $ i $ to all possible values. As we sum over $ i $ anyway, this cancels out with $1/N!$.
So we have:
\begin{gather}
\text{one-electron in} \langle \psi \lvert H_e \lvert \psi \rangle =
\sum_i \int dx \cdot \varphi^*_i(x)
\bigr( \frac{\mathbf{p}^2}{2m_e} – V_{\text{nucl}}(\mathbf{r}) \bigl)
\varphi_i(x)
\end{gather}
Two-particle contribution
Likewise, we may simplify the two-particle contribution. The integrals of the untouched orbitals will give us again $ \delta_{\nu n,\mu n} $. But this time, this still leaves two possible permutations for the touched orbitals $i, j$:
1) $ \nu(i) = \mu(i) $ and $ \nu(j) = \mu(j) $, meaning they are identical and $ \text{sign}(\nu) \cdot \text{sign}(\mu) = 1 $
2) $ \nu(i) = \mu(j) $ and $ \nu(j) = \mu(i) $, meaning $\nu$ and $\mu$ differ by one swap and give $ \text{sign}(\nu) \cdot \text{sign}(\mu) = -1 $.
Again, this takes care of the first summation over all permutations. The second summation, together with the sum over all $ i \neq j $, produces $ N! $ identical terms.
\begin{align}
\text{two-electrons in} \langle \psi \lvert H_e \lvert \psi \rangle = &
\sum_{i \neq j} \int dx dx’ \cdot \frac{e^2}{|\mathbf{r} – \mathbf{r’} |} \\
& \bigr( \varphi^*_i(x) \varphi^*_j(x’) \cdot \varphi_i(x) \varphi_j(x’) \\
& \quad – \varphi^*_i(x) \varphi^*_j(x’) \cdot \varphi_i(x’) \varphi_j(x)
\bigl)
\end{align}
The variation of the functional $ E_0[\varphi^*_k] $ above on $ \delta \varphi^*_k $ now leads to the Hartree-Fock equations:
Hartree-Fock equations
\begin{gather}
\bigr( \frac{\mathbf{p}^2}{2m_e} – V_{\text{nucl}}(\mathbf{r})
+ \sum_{j \neq k} \int dx’ \cdot \frac{e^2}{|\mathbf{r} – \mathbf{r’} |} \varphi^*_j(x’) \cdot \varphi_j(x’) \bigl) \varphi_k(x) \\
– \sum_{j \neq k} \int dx’ \cdot \frac{e^2}{|\mathbf{r} – \mathbf{r’} |} \varphi^*_j(x’) \varphi_j(x) \frac{\varphi_k(x’)}{\varphi_k(x)} \cdot \varphi_k(x) = \epsilon_k \varphi_k(x)
\end{gather}
The first two-electron term may be interpreted as a Coulomb repulsion of an electron $k$ at the position $ \mathbf{r} $ due to the presence of all the other electrons.
The second two-electron term is due to the Pauli exclusion principle. It is called the exchange potential and is a non-local term, as the spin-orbital $ \varphi_k(x’) $ is part of the integration kernel over $x’$. Here, we ignore this problem and deal with it in the main text by using the self-consistent field method.
Now it’s time to resolve our notational convention:
\begin{gather}
x := (\mathbf{r}, s) \text{ and } x’ := (\mathbf{r’}, s’) \\
\int dx’ := \sum_{s’} \int d^3 r’
\end{gather}
and also take into account, that summation indices and the spin orbitals factor in a spatial and a spin part
\begin{gather}
j := (\mathbf{j}, \alpha) \text{ and } k := (\mathbf{k}, \beta) \\
\varphi_j(x) := \varphi_\mathbf{j}(\mathbf{r}) \cdot \sigma_\alpha(s)
\end{gather}
For the Coulomb potential we integrate over $ \varphi^{*}_j(x’) \cdot \varphi_j(x’) $ over $x’$. As the spin-orbitals factor as shown above, so does the integration. The integration of the $\sigma$’s gives us $=1$. We are left with integrals over the spatial part of the orbitals. Additionally the spin part of the summation indices gives a factor $=2$.
For the exchange potential we integrate $\varphi^{*}_j(x’) \cdot \varphi_k(x’)$ over $x’$. This time, we have to closely pay attention to the integrals over the spin-part: Only those terms of $\varphi^{*}_j$ contribute, that are polarized with spins parallel to $\varphi_k $ xx.
The resulting eigenequation may be written in a compact form:
\begin{gather}
F \varphi_k = \epsilon_k \varphi_k \\
\text{with} \\
F = \sum_i^{\text{occ}} \bigl( \frac{\mathbf{p}_i^2}{2m_e} – V_{\text{nucl}}(\mathbf{r_i}) \bigr) +
\sum_i^{\text{occ}} \bigl( 2 J_i – K^{polar}_i\bigr)
\end{gather}
7 Footnotes
i1 In this formulation we have set a whole bunch of constants to 1. Generally, the two-body system of the nucleus and electron rotate around a center of mass. Due to the very large mass of the nucleus, we have neglected this fact and placed the COM into the nucleus.
i2 For example, a spherical and centralized system like an atom has a rotational symmetry. The related rotation group in $\mathbb{R}^3$ is generated by the rotational Lie algebra . The associated conserved angular momentum is this set of generators.
Thus, the first eigenequation above will give us all irreducable representations of the rotational Lie algebra in our Hilbert space (you may find out more about irreducable representations in the appendix of my article “From Shor to the Quantum Hidden Subgroup Problem – A jumpstart”).
This is how it works:
The spatial components $L_x, L_y, L_z$ of the angular momentum follow the same commutation rules as the rotational Lie algebra $ [L_i, L_j] = i \epsilon_{ijk} \hbar \cdot L_k $ (we just ignore the constant factor $ \hbar $ in this discussion for simplicity). Thus, to find the rotational irreducable representations in our Hilbert space, we just need to find the representations of the $L_x, L_y, L_z$. All eigenstates of $ L^2 $ may be labeled by $l$.
Each eigenvalue is degenerate, so for each $ l $ there will be a subspace of eigenstates. How does the structure of the $ L_i $ look like in each $l$-subspace? The different components $L_i$ do not commute, but each one commutes with $ L^2 $. This means: All the $L_i$ are block diagonal in the $l$-subspaces. These blocks are exactly the irreducable representations of the Lie algebra of the rotational group!
For each $l$-subspace, we may fix one $ L_i $. compute its eigenvalues and eigenstates to find and label an suitable basis for the $l$-subspace. Per convention this is $ L_z $:
\begin{align}
L^2 \lvert l, m \rangle &= \hbar^2 l(l+1) \lvert l, m \rangle \\
\text{and} \\
L_z \lvert l, m \rangle &= \hbar m \lvert l, m \rangle \quad \text{with} -l\le m \le +l
\end{align}
i3 https://vixra.org/abs/1701.0299: “A Child’s Guide to Spinors” by W. Straub
ii https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Introductory_Chemistry_(CK-12)/03%3A_Measurements/3.12%3A_Accuracy_and_Precision: About the difference between accuracy and precision
iii https://en.wikipedia.org/wiki/Born%E2%80%93Oppenheimer_approximation: About the Botn-Oppenheimer approximation on Wikipedia
iv https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Mechanics__in_Chemistry_(Simons_and_Nichols): “Quantum Mechanics in Chemistry” by Simons and Nichols, University of Utah
v https://www.youtube.com/watch?v=43Kd3yUG5io&list=PLkNVwyLvX_TFBLHCvApmvafqqQUHb6JwF&index=16: “CompChem.04.01 Ab Initio Hartree-Fock Theory: Basis Sets and LCAO Wave Functions”, by Chris Cramer on YouTube
vi https://pubs.aip.org/aip/jcp/article-abstract/90/2/1007/91329/Gaussian-basis-sets-for-use-in-correlated?redirectedFrom=fulltext: “Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen” (1989) by Thom H. Dunning, Jr.
vii https://onlinelibrary.wiley.com/doi/10.1002/qua.24355: “Gaussian basis sets for molecular applications” by J. Grant
ix https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Mechanics__in_Chemistry_(Simons_and_Nichols): “Quantum Mechanics in Chemistry” by Simons and Nichols University of Utah.
x http://vergil.chemistry.gatech.edu/notes/df.pdf: “Density-Fitting Approximations to the Electron Repulsion Integrals”, C. Sherrill, Georgia Institute of Technology
xi http://wild.life.nctu.edu.tw/class/common/energy-unit-conv-table.html: A Conversion table for different units
xii https://www.youtube.com/watch?v=5BZxa6fZHZU&list=PLkNVwyLvX_TFBLHCvApmvafqqQUHb6JwF&index=18: “CompChem.04.02 Post-Hartree-Fock Theory: Electron Correlation and Configuration Interaction“ by Chris Cramer on YouTube
xiii See “Quantum Mechanics in Chemistry” chapter 19 for details about the groundstate of the Be-atom (see above).
xiv https://www.youtube.com/watch?v=SThFgfJLXMk: “VK 20 WF 2: Configuration interaction and MCSCF” by Stephan P. A. Sauer on YouTube
xv https://pubs.acs.org/doi/10.1021/acs.jctc.3c01190?goto=recommendations&?ref=pdf: “Distributed Implementation of Full Configuration Interaction for One Trillion Determinants” by Hong Gao, Satoshi Imamura, Akihiko Kasagi, and Eiji Yoshida, Journal of Chemical Theory and Computation 2024
xvi http://myweb.liu.edu/~nmatsuna/gamess/refs/how.to.ci.html: by Nikita Matsunaga
xvii Chapter 10 in “Quantum Mechanics in Chemistry” by Simons and Nichols (see above)
xviii “AN INTRODUCTION TO MCSCF: PART 2” by Mark Gordon, Ames Laboratory/Iowa State University
xix https://www.home.uni-osnabrueck.de/apostnik/Lectures/DFT-2.pdf: “Hartree-Fock formalism” by Andrei Postnikov
xx https://itp.tugraz.at/LV/ewald/TFKP/Kapitel_8SHORTn.pdf: “Kapitel 8 Das Hartree – Fock Verfahren”