Quantum chemistry is one of the top most promising and one of the first applications for quantum computing. Most likely, the success in quantum chemistry will serve as a reliable “early-alerting indicator” for other potential applications. Thus, staying up to date to the developments in chemistry is important for the entire quantum computing community!
Part I of this article series introduced many technical concepts and terms of traditional quantum chemistry that you need to now to master the quantum computing literature.
This part II introduces several important and advanced Post-Hartree-Fock methods for classical computation, that enter the ring with quantum computing strategies.
Contents
- 1 Introduction
- 2 Second Quantization and Quantum Computing
- 3 Post-Hartree-Fock II: MCSCF, Coupled Cluster, Pertubation Theory, CCSD(T) and DMRG
- 3.1 The Multiconfiguration Self Consistent Field method MCSCF II
- 3.2 The Coupled Cluster method in Quantum Chemistry
- 3.3 Møller-Plesset and Coupled Cluster Pertubation Theory in quantum chemistry
- 3.4 CCSD(T): The “gold standard” of Quantum Chemistry
- 3.5 The scaling of Post-Hartree-Fock methods
- 3.6 The Density Matrix Renormalization Group (DMRG) in Quantum Chemistry
- 6 Appendices
- 7 Footnotes
1 Introduction
1.1 Quantum chemistry
The chemical industry is one of the top most promising target fields for quantum computers. Quantum computing seems favorable for chemical problems for several technical reasons. It is expected, that even small quantum computers could have a relevant impact for the industry. Thus, chemistry will probably serve as a reliable “early-alerting indicator” for the success of quantum computing. Staying up to date to these developments will be important for the whole community!
My opinion about chemistry and quantum computing is: If we can’t make it there, we can’t make it anywhere.
But quantum chemistry is a very mature branch of science and its quantum computing papers are packed with technical terms and concepts from traditional quantum chemistry. Part I of this article series introduced to many of those aspects. For educational reasons, I have saved one important aspect for this article: An introduction to second quantization along with a brief insight into quantum computation for chemistry.
These qc-algorithms enter the ring with cutting-edge strategies to approximate the electronic structure problem using digital computation. I have introduced the most basic method, the Hartree-Fock method, in the first article of this series. But advanced strategies are “post-Hartree-Fock”. We have already learned about the Full Configuration Interaction.
1.2 About this article

This article introduces even more advanced Post-Hartree-Fock-methods, to get an impression of their strengths and weaknesses:
- What are their underlying concepts?
- How do their fundamental equations actually look like?
- How are they solved?
- What is their scaling?
- Some cutting-edge examples, that have been carried out
To be precise, you will learn the following aspects:
- Introduction to Second Quantization
- A detour to Quantum computing for chemistry: About the Jordan-Wigner transformation, the Aspuru-Guzik / Whitfield-method and a roadblock for VQE
- Multireference, the MCSCF- and CASSCF-methods and optimizing molecular orbitals
- Coupled Cluster theory and Coupled Cluster Pertubation theory
- Møller-Plesset perturbation theory
- CCSD(T): The “gold standard” of quantum chemistry and some concrete equations for its 4th and 5th order corrections
- DMRG, exploiting quasi 1-dimensional systems
- Scalings, examples / limits
While I recommend you to read part I first, this article completes my introduction to quantum chemistry for quantum computing enthusiasts.
2 Second Quantization and Quantum Computing
2.1 Second Quantization in a Nutshell
Before we get into the details of the various Post-Hartree-Fock methods we have to master another technical tool, just like we have mastered Slater determinants in part I of this series. It is a fundamental ground work for all quantum field theories. More important for us: It sets the stage for quantum computing algorithms in quantum chemistry.
The Fock space
So far, we have used a specific formulation of the Hilbert space, operators and wavefunctions, which is called first quantization. To deal with identical fermionic particles we had to introduce Slater determinants. In particular, first quantization fixes the particle numbers. This is specifically very bad for high-energy physics, where particles are constantly created and destroyed (like photons, gluons, pairs of electrons and anti-electrons or quarks and anti-quarks, products of particle-collisions, …).
More important for us: For carrying out quantum computation in chemistry, we need to have a much more efficient representation of our chemical system to restrict our calculation to as few qubits as possible. And here we go:
Second quantization lifts our notation for electron configurations to a formal principle. Using its occupation number representation multi-particle states are a superposition of the following abstract basis states i:
\begin{gather}
\lvert \mathbf{n} \rangle = \lvert n_1, n_2, n_3, \ldots \rangle
\end{gather}
In there, the occupation numbers $n_i$ are natural numbers, that describe how many particles are in the state $\lvert i \rangle$. These states will always be (molecular) spin-orbitals in our case. Specifically, for fermions (e.g. electrons) is $ n_i = 0 $ or $ n_i = 1 $, because of the Pauli-principle. The corresponding Hilbert space in second quantization is called the Fock space. We note, that the fermionic basis states $\lvert \mathbf{n} \rangle$ have a very “qubit-friendly” structure, made up by a string of zeros and ones.
The vacuum-state is defined as:
\begin{gather}
\lvert \text{vac} \rangle = \lvert 0, 0, 0, \ldots, 0 \rangle
\end{gather}
Creation and annihilation operators
Along the occupation number representation comes a family of very important operators, that execute transformations between these basis states. The creation operators $a^\dagger_i$ increase the occupation number of the i’th state / spin-orbital by 1. For our fermionic case, we can increase only $n_i = 0$ to $ n_i = 1$. Executing $a^\dagger_i$ twice will give us the null-vector:
\begin{align}
a^\dagger_i \lvert n_1, n_2, \ldots, n_{i-1}, 0_i, n_{i+1}, \ldots \rangle =& \Gamma^{n}_i \cdot \lvert n_1, n_2, \ldots, n_{i-1}, 1_i, n_{i+1}, \ldots \rangle \\
a^\dagger_i \lvert n_1, n_2, \ldots, n_{i-1}, 1_i, n_{i+1}, \ldots \rangle =& 0 \\
\text{with the phase phactor } \Gamma^{n}_i =& \prod_{k<i} (-1)^{n_k}
\end{align}
Thus, the phase factor $\Gamma$ “collects” a minus-factor for each occupied spin-orbital left of $i$.
Each occupation number basis state may be created from the vacuum-state by a series of creation operators:
\begin{align}
\lvert \mathbf{n} \rangle = \prod_i \left( a^\dagger_i \right)^{n_i} \lvert \text{vac} \rangle
\end{align}
Likewise, the annihilation operators $a_i$ work in the opposite way, they decrease the occupation number:
\begin{align}
a_i \lvert n_1, n_2, \ldots, n_{i-1}, 1_i, n_{i+1}, \ldots \rangle =& \Gamma^{n}_i \cdot \lvert n_1, n_2, \ldots, n_{i-1}, 0_i, n_{i+1}, \ldots \rangle \\
a_i \lvert n_1, n_2, \ldots, n_{i-1}, 0_i, n_{i+1}, \ldots \rangle =& 0
\end{align}
The complicated antisymmetric structure of the Slater determinants are now reduced to simple anticommutation rules of the creation and annihilation operators:
\begin{align}
\left\{a_i, a_j\right\} & :=a_i a_j + a_j a_i =& 0 \\
\left\{a^\dagger_i, a^\dagger_j\right\} & :=a^\dagger_i a^\dagger_j + a^\dagger_j a^\dagger_i =& 0 \\
\left\{a^\dagger_i, a_j\right\} &:=a^\dagger_i a_j + a_j a^\dagger_i =& \delta_{ij}
\end{align}
The occupation number operator gives us the number of particles, that occupy the spin-orbital $ i$:
\begin{align}
N_i =& a^\dagger_i a_i \\
N_i \lvert \mathbf{n} \rangle =& N \lvert n_1, n_2, \ldots \rangle = \delta_{n_i1} \lvert n \rangle = n_i \lvert n \rangle
\end{align}
Just as a fun fact: Nowadays the term “second quantization” is regarded as a misnomer which has survived for historical reasons. The creation and annihilation operators introduce a new interpretation of identical particles as an operator valued “particle-field”, which was necessary to derive quantum field theories like quantum electrodynamics:
The modes of the classical electromagnetic field are created and annihilated using the framework of second quantization and materialize in quantized particles — the photons. Following this concept, the modes of the electron (its wavefunctions) establish a quantized electron-field $ \sum_i \psi_i(x, t) \cdot a^\dagger_i$. As the electronic wavefunctions are the result of the prior “first quantization” it appears as if we are quantizing again. Contrary, nowadays the wavefunctions in quantum field theory are rather interpreted as a solution of a semi-classical field equation.
See the Wikipedia-article on “Second quantization” ii.
2.2 Electronic structure Hamiltonian in Second Quantization
Now, by using the occupation number representation, we may express the electronic structure Hamiltonian in a simple algebraic form. This makes it much more convenient for doing quantum computation, as we will see shortly:
In second quantization, the Born-Oppenheimer-approximation reduces to:
\begin{align}
H = \sum_{r,s} h_{rs} \cdot a^\dagger_r a_s +
\frac{1}{2} \sum_{p,q,r,s} g_{pqrs} \cdot a^\dagger_p a^\dagger_r a_q a_s
\end{align}
with
\begin{align}
h_{rs} &= \int dx \cdot \varphi_r^*(x) \left( \frac{\mathbf{r}^2}{2m_e} – \sum_i V_{\text{nucl}}(\mathbf{R_i}-\mathbf{r}) \right) \varphi_s(x) \\
g_{pqrs} &= \int dx_1 dx_2 \cdot \varphi_p^*(x_1) \varphi_r^*(x_2) \left( \frac{e^2}{|\mathbf{r_1} – \mathbf{r_2}|} \right) \varphi_q(x_1) \varphi_s(x_2)
\end{align}
and again, we have used the notation
\begin{gather}
x_i := (\mathbf{r}_i, s_i)
\end{gather}
Of course, the $ \varphi_i $ are just the spin-orbitals from first quantization.
By the way: Many authors also like the “Mulliken notation”
\begin{gather}
g_{pqrs} =: \left(pq \lvert rs \right)
\end{gather}
Note, that all indices $p,q,r$ and $s$ run over all spin-orbitals of the chosen one-particle Hilbert space. Usually, this will be the canonical molecular orbitals of a prior Hartree-Fock calculation that you have learned about in part I of this series.
- The number of occupied orbitals is fixed by the number of electrons.
- The number of virtual orbitals is dictated by the number of functions in the basis set, e.g. its “zeta-depth”.
The integrals $ h_{rs} $ and $ \left(pq \lvert rs \right) $ are computed by the molecular orbitals’ expansions into the set of contracted Gaussian primitive functions of the chosen basis set.
2.3 Quantum Chemistry and Quantum Computing in a Nutshell
Quantum Phase Estimation
The Hamiltonian above is the starting point of several strategies to map chemical problems onto a quantum computer. It was first proposed by Abrams and Lloyd in 1997. In two other landmark papers Aspuru-Guzik (2006) and Whitfield et. al (2010) took this idea even further to solve the molecular energy problem on a quantum computer iii iv v vi.
Back then it was assumed, that these methods provide an exponential speedup compared to the FCI-method. Today this “Exponential Quantum Advantage Hypothesis“ for Quantum Chemistry is questioned. See my article Challenging the “Exponential Quantum Advantage Hypothesis“ for Quantum Chemistry on this issue for details.
The general idea of Aspuru-Guzik’s algorithm goes like this:
- Step 1. Choose a high quality basis set to achieve a certain degree of accuracy.
- Step 2. Calculate the one-body- and two-body-integrals of the Hamiltonian above
- Step 3. Map the (local) creation and annihilation operators to strings of Pauli-operators that fullfill the same anti-commutation relations. This generates an expansion of the Hamiltonian into many terms of different Pauli-strings.
- Step 4. Estimate the ground state energy of this system using quantum phase estimation and the Trotter decomposition.
The Jordan-Wigner-transformation
Step 3 is a crucial step: It trades the super efficient mapping of spin-orbitals to simple qubits for the costly mapping of simple, local creation and annihilation operators to complex, non-local strings of Pauli-operators. All in all this is still an efficient strategy.
For this step Whitfield introduced the well-known Jordan-Wigner-transformation:
\begin{align}
a^\dagger_p =& \left(\prod_{k<p} \sigma_k^z \right) \sigma_p^+ \\
a_p =& \left(\prod_{k<p} \sigma_k^z \right) \sigma_p^- \\
\text{with } \sigma_p^\pm =& \left(\sigma^x \mp i\sigma^y \right)/2
\end{align}
So just as with the $\Gamma$-factor above, the Jordan-Wigner-transform “collects” a $\sigma^z$-factor for each qubit left of $p$ and thus a minus-phase for each occupied spin-orbital left of $p$.
Software libraries
Just as in our simple PySCF-script in part I of this series, modern quantum computing frameworks like Qiskit Nature, OpenFermion and Pennylane abstract away all the gory technical details of this strategy.
The following example shows an implementation of the Hamiltonian for a water molecule in second quantization via Jordan-Wigner-transformation using Qiskit Nature and its PySCF-bridge:
driver = PySCFDriver(atom="O 0 0 0; H 0 1 0; H 0 0 1", basis="6-31G", charge=0, spin=0, unit=DistanceUnit.ANGSTROM ) problem = driver.run() hamiltonian = problem.hamiltonian coefficients = hamiltonian.electronic_integrals print(coefficients) second_q_op = hamiltonian.second_q_op() mapper = JordanWignerMapper() qubit_jw_op = mapper.map(second_q_op) print(qubit_jw_op)
Pretty nice, right? 🙂
But the is just a side remark and you will find many very good and handy tutorials if you scan the documentation of the quantum computing frameworks, that I have mentioned above.
But wait! There is one problem for near term quantum computation, that I want to mention at this point:
A Roadblock for VQE-strategies
The result of the listing above will actually generate 26 spin orbitals and the Hamiltonian is expanded into 36 000 Pauli-strings. And this is just for the STO-6-31G basis … When we use the larger double-zeta basis cc-pVDZ, we get 48 spin orbitals and 354 000 Pauli-strings! If we aim for chemical accuracy probably even cc-pVTZ would not be enough, which already crashes my Python-runtime.
This poses a serious problem for measuring the expectation value of a trial wavefunction on a quantum computer as in the VQE-algorithm for NISQ-devices:
\begin{gather}
E_0 \leq \frac{ \langle \psi_{\text{trial}} \lvert H_e \lvert \psi_{\text{trial}} \rangle }{\langle \psi_{\text{trial}} \lvert \psi_{\text{trial}} \rangle}
\end{gather}
In order to measure the expectation value of the non-unitary Hamiltonian, we need to measure the individual expectation values of each Pauli-string term in the expansion. There exist remarkable strategies to group these Pauli-strings, such that each group requires only a single measurement. See the nice PennyLane-introduction to qubit-wise commuting Pauli-terms for this matter vii.
Yet, it is estimated, that this is not enough to reach chemical accuracy $ \epsilon$. An amount of $K / \epsilon^2$ measurements is needed, where $K$ is a constant depending on the Pauli-grouped Hamiltonian and thus, also on the basis set chosen. This has been carried out in detail viii.
For rather small hydrocarbons (methane, methanol, …) a wall-clock runtimes of days were predicted.
But this was just a detour. Let’s get back to traditional quantum chemistry for digital computers.
3 Post-Hartree-Fock II: MCSCF, Coupled Cluster, Pertubation Theory, CCSD(T) and DMRG
Part I of this article series finished with an informal introduction to the Multiconfiguration Self Consistent Field method. I promised to outline the basic details of the theory after introducing second quantization.
Well, now that the latter is done: Here we go …
3.1 The Multiconfiguration Self Consistent Field method MCSCF II
Most textbooks don’t go deep into MCSCF-methods … you will soon see why.
In particular, it is hard to find a detailed and up to date introduction online. I found the PhD-thesis “Multiconfiguration self-consistent field methods for large molecules” by David Kreplin very insightful. In the following I summarize some of his derivations and added a few comments ix:
Using the Hamiltonian in second quantization representation, we are able to write down all equations that are relevant for the multiconfiguration self consistent field method. Remember, MCSCF uses a two-fold optimization strategy:
- In the outer optimization loop, we optimize the CI-coefficients like explained in part I of this series. After we have calculated these coefficients, we start …
- … The inner optimization loop: We fix the CI-coefficients and vary the molecular orbitals (which we had fixed before) using a self consistent field method. Now we have a set of improved molecular orbitals.
- Then we start the next iteration: We continue with the outer loop and do another CI-optimization, using the fixed and improved configurations. We obtain a new set of CI-coefficients, that we fix to continue with the inner loop: Another variation of the molecular orbitals.
- … We keep on going until our method converges.
This sounds highly complicated … and it is. We will have to introduce lots of optimization parameters. Yet, it is astonishing, that one is able to formulate all of this in closed forms. To achieve this, we will also have to introduce a few short hand notations though … quite a few actually! In part I of this series, we did not look closer into the Full CI matrix. Now, we will spell it out more explicitely and analyze the molecular orbital optimization later.
First of all, we distinguish between $\alpha$- and $\beta$-spins by labeling the creation and annihilation operator of the spin-orbitals with $\beta$-spins by an extra bar $\bar{a}^\dagger_r$ and $\bar{a}_r$. Next, we introduce the “excitation operators”
\begin{align}
E_{rs} :=& a^\dagger_r a_s + \bar{a}^\dagger_r \bar{a}_s \\
E_{pqrs} :=& a^\dagger_p E_{rs} a_q + \bar{a}^\dagger_p E_{rs} \bar{a}_q = E_{pq} E_{rs} – \delta_{qr} E_{ps}
\end{align}
These excitation operators reflect again the fact, that we expect the spin orbitals to factor into a spatial and a spin parts. This makes our Hamiltonian:
\begin{align}
H = \sum_{r,s} h_{rs} \cdot E_{rs} +
\frac{1}{2} \sum_{p,q,r,s} \left(pq \lvert rs \right) \cdot E_{pqrs}
\end{align}
MCSCF: Optimizing the CI-coefficients
We want to express this as a matrix in the CI-basis $\Phi_I$. Remember, that our state may be written as a CI-expansion:
\begin{align}
\lvert \Psi \rangle = \sum_{I} c_I \lvert \Phi_I \rangle
\end{align}
In the part I of this series, we constructed the $\Phi_I$, by gradually replacing occupied by virtual molecular spin-orbitals. Using Slater determinants, this looked kind of wild. Now, we are able to reformulate this, using the framework of second quantization:
\begin{align}
\lvert \Phi_k^a \rangle = a^\dagger_a a_k \cdot \lvert HF \rangle , \quad \lvert \Phi_{k l}^{a b} \rangle = a^\dagger_a a_k \cdot a^\dagger_b a_l \cdot \lvert HF \rangle . \quad \ldots
\end{align}
If we work with CSFs instead, the $\Phi_I$ are contractions / fixed superpositions of the states above.
By using the excitation operators $ E $, we introduce the coupling coefficients:
\begin{align}
\gamma^{IJ}_{rs} := \langle \Phi_I \lvert E_{rs} \lvert \Phi_J \rangle \quad \text{ and } \quad \Gamma^{IJ}_{pqrs} := \langle \Phi_I \lvert E_{pqrs} \lvert \Phi_J \rangle
\end{align}
Indeed, these couple / constraint the indices of the molecular orbitals $ p, q, r, s $ to the indices $ I, J $ of the CI-expansion. E.g. if the spin-orbital $ r $ is not present in $ \Phi_I $, then we get $ \gamma^{IJ}_{rs} = 0 $.
By the way, as $ E_{pqrs} $ may be expressed as a sum of $E_{rs}$ and $E_{pq} $, the $\Gamma$ may be expressed as a sum of a bunch of $\gamma$’s (using the resolution of identity).
Now, we get a more explicit form of the Hamiltonian-matrix for Full CI:
\begin{align}
H_{IJ} = \sum_{r,s} h_{rs} \cdot \gamma^{IJ}_{rs} +
\frac{1}{2} \sum_{p,q,r,s} \left(pq \lvert rs \right) \cdot \Gamma^{IJ}_{pqrs}
\end{align}
As a sidenote: At this point we are only interested in the CI-optimization. But later, for the orbital optimization, we will have to pay close attention to how the $ \gamma^{IJ}_{rs} $ and $ \Gamma^{IJ}_{pqrs} $ transform during optimization by using our orbital parameterization.
Like in Full CI the secular equation gives us the linear algebraic equation:
\begin{align}
\sum_J H_{IJ} \cdot c_J – E \cdot c_I = 0
\end{align}
The Complete Active Space approach / CASSCF
The MCSCF method simplifies the Full CI-equation above by considering only those CI-functions $\Phi_I$ which contribute the most to the matrix. The most common strategy is to analyze all CI-functions in a complete active space (CAS), making it the CASSCF method. The CAS is an active space with $N_{el}$ electrons and $N_{act}$ “active” spatial orbitals
CAS($N_{el}, N_{act}$).
Although this reduces the complexity of the Full CI approach significantly, the active space of the CAS-strategy also results in an exponential scaling. One reduces this further by noting, that probably not all active setups are equally alike. Problably, single excitations contribute much more than excitations of all $N_{el}$ CAS-electrons. Also, the higher virtual orbitals will contribute less than the lowest virtual MO.
By systematically restricting the CAS one ends up with the restricted active space method (RASSCF).
MCSCF-Hamiltonian and MCSCF-Energy function
Following Kreplin’s notation we name the summation indices according to their CAS-relationship:
- $r, s, p, q$: Referring to all molecular orbitals (MOs)
- $i, j$: Referring to inactive orbitals (or closed-shell, MOs doubly occupied in all configurations)
- $t, u, v, w$: Referring to active orbitals (MOs with varying occupations)
- $k, l$: Referring to occupied MOs
- $a, b$: Referring to virtual orbitals (non-occupied MOs)
Using this naming convention, we are able to strip off the inactive, closed shell contributions from the active ones:
\begin{align}
H_{IJ} = \delta_{IJ} E_c + \sum_{tu}^\text{act} F_{tu}^c \cdot \gamma^{IJ}_{tu} +
\frac{1}{2} \sum_{tuvw}^\text{act} \left(tu \lvert vw \right) \cdot \Gamma^{IJ}_{tuvw}
\end{align}
Here we have seperated the contribution of the closed-shell orbitals using the closed-shell energy $E_c$ and the closed-shell Fock matrix $F_{rs}^c$:
\begin{align}
E_c := \sum_i^{cs} \left( h_{ii} + F_{ii}^c \right)
\quad \text{ and } \quad
F_{rs}^c := h_{rs} + \sum_i^{cs} \left( 2J_{rs}^{ii} – K_{rs}^{ii} \right)
\end{align}
$J$ and $K$ are the matrix representations of the Coulomb integral and the exchange integral
\begin{align}
J_{rs}^{kl} := \left(kl \lvert rs \right)
\quad \text{ and } \quad
K_{rs}^{kl} := \left(rk \lvert ls \right)
\end{align}
The evaluated coupling coefficients $\gamma$ and $\Gamma$ allow us to rewrite the energy $E = c^T H c$ for a given set of CI coefficients $c$:
\begin{align}
E = E_c + \sum_{tu}^\text{act} F_{tu}^c \cdot D_{tu} +
\frac{1}{2} \sum_{tuvw}^\text{act} \left(tu \lvert vw \right) \cdot D_{tuvw}
\end{align}
The coupling coefficients are contracted with the given CI vector and we get the active one- and two-particle reduced density matrices :
\begin{align}
D_{tu} := \sum_{IJ} c_I \cdot \gamma^{IJ}_{tu} \cdot c_J
\quad \text{ and } \quad
D_{tuvw} := \sum_{IJ} c_I \cdot \Gamma^{IJ}_{tuvw} \cdot c_J
\end{align}
Note, that the reduced density matrices are quadratic functions of the CI-coefficients.
You may also find this formula in “Quantum Mechanics in Chemistry” by Simons and Nichols chapter 18 x along with an informal description of the reduced density matrices. I summarized it in the footnote for you xi.
MCSCF: Varying the Molecular orbitals
In the Hartree-Fock method we were able to convert the optimizing problem for the molecular orbitals into a linear algebra problem. For the general MCSCF-method this is not possible. Instead, one needs to use approximation techniques to minimize the energy. A common strategy is the iterative Newton Raphson method (NR) : To find the minimum of a function $f$, a root of the first derivative $f’$, one approximates the derivative at a starting point $x_0$ with its tangent (also known as the derivative’s first order Taylor expansion):
\begin{align}
t(x) = f'(x_0) + f”(x_0) \cdot (x-x_0)
\end{align}
The root of this tangent is a good candidate for the next optimization step:
\begin{align}
x_1 = x_0 – \frac{f'(x_0)}{f”(x_0)}
\end{align}
For a function in higher dimensions one needs its gradient and Hessian as first and second derivative.
So, for our energy function we need to find a nice way to parameterize the transformation of the molecular orbitals and then find its gradient and Hessian using this parameterization.
As usual our molecular orbitals $(\varphi_r)_r $ are expressed using a specific basis set of atomic orbitals $(\chi_{\mu})_{\mu} $:
\begin{align}
\varphi_r = \sum_{\mu} \chi_{\mu} \cdot M_{r\mu}
\end{align}
By optimizing the molecular orbitals $(\varphi_r’)_r $, we transform (the real-valued) $(\varphi_r)_r $ by an orthogonal matrix $U$
\begin{align}
\varphi_r’ = U \varphi_r
\end{align}
According to basic linear algebra, on orthogonal $U$ may be expressed by an antisymmetric matrix $R$:
\begin{align}
U = exp(R) = 1 + R + \frac{1}{2!}R^2 + \frac{1}{3!}R^3 + \ldots
\end{align}
We may expand $R$ using our excitation operators from above:
\begin{align}
R = \sum_{r>k} R_{rk} \left( E_{rk} – E_{kr} \right)
\end{align}
These rotations are our parameterization. They transform the reduced density matrices via
\begin{align}
D_{tu} = \sum_{IJ} c_I \cdot \gamma^{IJ}_{tu} \cdot c_J \rightarrow \sum_{IJ} c_I \cdot \langle \Phi_I \lvert exp(-R) \cdot E_{tu} \cdot exp(R) \lvert \Phi_J \rangle \cdot c_J
\end{align}
We may carry out the Newton-Raphson optimization by calculating the gradient and the Hessian as derivatives of the parameterized energy function with variable $R$. The calculation may be carried out by Taylor-expanding the energy function with respect to the scalar $R_{rk}$ and collecting first and second order terms. If you are up to the challenge, I will sketch this calculation in the Appendix 2: The orbital optimization in MCSCF for you.
Of course, this is just the beginning of the MCSCF method. Starting from here, one analyzes different convergence strategies and approximation techniques as discussed in Kreplin’s thesis. Have fun reading 🙂
MCSCF: Computational limits
The MCSCF-method also highlights the potential of chemical methods in quantum computation. Calculations of an active space of order (20, 20) and over a billion CSF are considered state of the art, using massively parallel classical computations.
The authors in “Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations” xii benchmark a single MCSCF-iteration for the $ \text{Cr}_3 $-molecule using a (20, 20)-CAS with a STO 6-31G basis. They scale there parallalization technique on different hardware-setups, from 32 to 512 cores reaching single iteration runtime from 10 to 1½ hours.
Yet, to reach chemical accuracy one would probably rather need to target triple-zeta basis sets such as cc-pVTZ as stated in “How will quantum computers provide an industrially relevant computational advantage in quantum chemistry?” xiii.
There the authors also outline, that industrially relevant molecules for a quantum advantage would be rather in the range of a CAS(60, 60). They name “biomimetics” as a potential use case in this range. So which industrial applications might fit in a range of say from CAS(24,24) to CAS(60, 60)? For these ranges, the authors state, that varifying or training less rigorous chemical methods (such as Density functional theory) might benefit from exact calculations even for medium scales CAS-calculations on a quantum computer.
And by the way: Don’t you think, that we are starting to get pretty fit with chemical nomenclature by now?! 😉
3.2 The Coupled Cluster method in Quantum Chemistry
After we have discussed how to treat chemical problems with multireference character we are starting to get ready for the so-called “gold standard” of ab initio methods in quantum chemistry. This gold standard is an improved coupled cluster method, which shows several nice properties. So we need to get into coupled cluster theory first.
Again, just like for second quantization, we will rely on the nice introduction of the W. Klopper and D. Tew from University of Karlsruhe. It is a script of a lecture series. So it appears to be sketchy, but it actually covers many aspects of the theory but you should read it carefully. In the following sections I summarize its most important aspects and results and added a few comments xiv.
The Coupled Cluster Wavefunction
Again, the starting point of the coupled cluster method is the Hartree-Fock solution, this time in the second quantization framework:
\begin{align}
\lvert \text{HF} \rangle = \prod_i a^\dagger_i \lvert \text{vac} \rangle
\end{align}
Two electrons with spin orbitals $i, j$ experience a Coulomb repulsion. This disturbance is represented as superposition of excitations into virtual spin orbitals $a, b$
\begin{align}
a^\dagger_i a^\dagger_j \rightarrow a^\dagger_i a^\dagger_j + \sum_{a>b} t^{ab}_{ij} a^\dagger_a a^\dagger_b
\end{align}
Note, that we switched again to the notation $i, j, \ldots$ for indices of occupied orbitals as this matches the lecture script.
Next, we introduce a new operator $ \tau $
\begin{align}
\tau^{ab}_{ij} = a^\dagger_a a_i \cdot a^\dagger_b a_j
\end{align}
Now, we are able to write the excitation above in product form by remembering the fermionic properties of the annihilation and creation operators:
\begin{align}
\prod_{a>b} \left( 1 + t^{ab}_{ij} \cdot \tau^{ab}_{ij} \right) \lvert \text{vac} \rangle = a^\dagger_i a^\dagger_j \lvert \text{vac} \rangle + \sum_{a>b} t^{ab}_{ij} a^\dagger_a a^\dagger_b \lvert \text{vac} \rangle
\end{align}
This gives us the double coupled cluster wavefunction:
\begin{align}
\lvert \text{CCD} \rangle = \prod_{a>b, i>j} \left( 1 + t^{ab}_{ij} \cdot \tau^{ab}_{ij} \right) \lvert \text{HF} \rangle
\end{align}
We are able to extend this strategy, if we consider simultaneous interaction of a whole group $\mu$ of electrons:
\begin{align}
\tau_\mu := \tau^{abc…}_{ijk…} = a^\dagger_a a_i \cdot a^\dagger_b a_j \cdot a^\dagger_c a_k \cdots
\end{align}
This gives the general coupled cluster wavefunction :
\begin{align}
\lvert \text{CC} \rangle = \prod_{\mu} \left( 1 + t_{\mu} \cdot \tau_{\mu} \right) \lvert \text{HF} \rangle
\end{align}
The $ t_{\mu} $ are called the cluster amplitudes.
By the way: Note, that for the Full CI-wavefunction we could also use the operators $\tau$ which would give us an additive form:
\begin{align}
\lvert \text{CI} \rangle = \left( 1 + \sum_{\mu} c_{\mu} \cdot \tau_{\mu} \right) \lvert \text{HF} \rangle
\end{align}
As all the $\tau_\mu$ commute and $\tau_\mu^2 = 0$, we may even write the coupled cluster wavefunction in exponential form:
\begin{align}
\lvert \text{CC} \rangle &= \prod_{\mu} \left( 1 + t_{\mu} \cdot \tau_{\mu} \right) \lvert \text{HF} \rangle \\
&= \text{exp} \left( \sum_\mu t_{\mu} \cdot \tau_{\mu} \right) \lvert \text{HF} \rangle \\
&=: \text{exp} \left( T \right) \lvert \text{HF} \rangle
\end{align}
Using $T$ we may introduce the expansion of single, double, triple, … excitations. That is, we collect all related terms $\tau_\mu$:
\begin{align}
T = T_1 + T_2 + T_3 + \cdots
\end{align}
This gives us a natural truncation strategy for the coupled cluster method. This time, as we will see, this truncation will prove to be size consistent!
| CCS | $T_1$ |
| CCSD | $T_1 + T_2$ |
| CCSDT | $T_1 + T_2 + T_3$ |
| … | … |
This series rapidly converges, if the HF wavefunction is a good approximation.
The Coupled Cluster Equations
So, now that we introduced the coupled cluster wavefunction: How do we actually calculate it? The coupled cluster wavefunction is parameterized by the cluster amplitudes $t_\mu$. Could we just use the variational principles again? Unfortunately, this turns out to be computationally unfeasable. But there are other ways …
We start with the coupled cluster Schrödinger equation:
\begin{align}
H \lvert \text{CC} \rangle &= E \lvert \text{CC} \rangle \\
H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle &= E \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle \\
\end{align}
Every $T_i$ generates excited states, so projecting the Hartree-Fock state onto the coupled cluster wavefunction gives:
\begin{align}
\langle \text{HF} \lvert \text{exp} \left( T \right) = \langle \text{HF} \lvert
\end{align}
Using this, we could solve the coupled cluster Schrödinger equation again self consistently. But there is a better strategy:
For this, we introduce the similarity transformed Hamiltonian:
\begin{align}
H_T := \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right)
\end{align}
This decouples the energy and amplitude equation of the coupled cluster Hamiltonian and we get the coupled cluster equations
\begin{align}
\langle \text{HF} \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& E & \text{(1)} \\
\langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& 0 & \text{(2)}
\end{align}
We may get rid off the exponentials by using the commutations rules of the well-known Baker-Campbell-Hausdorff expansion. I will spare the details in the main text. Check the Appendix 3: Simplifying the Coupled Cluster Equations for the derivation.
This will show, that the energy expression in the first equation above depends directly only on the amplitudes of single and double excitations.
\begin{align}
E = E_\text{HF} + \langle \text{HF} \lvert [H,T_2] \lvert \text{HF} \rangle +
\frac{1}{2} \langle \text{HF} \lvert [[H,T_1],T_1] \lvert \text{HF} \rangle
\end{align}
But these amplitudes still depend on all the other amplitudes in a non-linear way because of the second coupled cluster equation. We will analyze this further.
Size consistency of the Coupled Cluster method
Before we discuss, how to solve the amplitude equation, let’s first check, if the coupled cluster equations are size consistent. As you probably remember, the truncated CI method was not size consistent.
We have two subsystems $A, B$ which decouple:
\begin{align}
H_{AB} =& H_A + H_B \\
\lvert \text{HF}_{AB} \rangle =& \lvert \text{HF}_{A} \rangle \lvert \text{HF}_{B} \rangle \\
H_{T,AB} =& \text{exp} \left( -T_A-T_B \right) \cdot \left(H_A + H_B)\right) \cdot \text{exp} \left( T_A+T_B \right) \\
=& H_{T,A} + H_{T,B}
\end{align}
Thus:
\begin{align}
E_{AB} =& \langle \text{HF}_{AB} \lvert H_{T,AB} \lvert \text{HF}_{AB} \rangle \\
=& \langle \text{HF}_{A} \lvert H_{T,A} \lvert \text{HF}_{A} \rangle
+ \langle \text{HF}_{B} \lvert H_{T,B} \lvert \text{HF}_{B} \rangle \\
=& E_A + E_B
\end{align}
And this works for arbitrary truncation levels for $ H_T $! This proves the size consistency.
Solving the Coupled Cluster Equations
To approximate the coupled cluster wavefunction, we start with the second coupled cluster equation. Here, I will just use the the general form of this amplitude equation. In the appendix 3 you will find an explicite equation for it:
\begin{align}
\langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle = 0
\end{align}
The left hand side of the equation may be interpreted as a highdimensional function of all the cluster amplitudes $t_\nu$, which we abbreviate as
\begin{align}
{\bf \Omega }({\bf t}) := \langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle
\end{align}
Looking at the BCH-expansion in appendix 3, we see that ${\bf \Omega }$ is a function at most quartic in the amplitudes. If we truncate the excitation operator $T = T_1 + T_2 $ to single and double excitations and $\lvert \mu \rangle $ to $\lvert \mu_1 \rangle $ and $\lvert \mu_2 \rangle $, we end up with the CCSD-approximation. This simplifies the amplitude equation similar to the general energy expression above. But we don’t get into the details here and focus on the solving the amplitude equation:
\begin{align}
{\bf \Omega }({\bf t}) = 0
\end{align}
Just like for the orbital-optimization in MCSCF the Newton Raphson method is a common starting point:
\begin{align}
0 = {\bf \Omega }({\bf t}^{(0)}) + {\bf \Omega }'({\bf t}^{(0)}) \cdot ({\bf t}-{\bf t}^{(0)})
\end{align}
But as ${\bf \Omega }$ is actually a highdimensional map with indices $\mu$ and variables $t_\nu$, we have to write this component-wise:
\begin{align}
\frac{\partial \Omega_\mu ({\bf t}^{(0)})}{\partial t_\nu} \cdot \left({t_\nu}^{(1)} – {t_\nu}^{(0)} \right) = – \Omega_\mu({\bf t}^{(0)})
\end{align}
This equation poses a problem: Although the Newton Raphson method itself tends to converge very quickly, we have to solve this linear equation in each iteration. As state-of-the-art coupled cluster computations have on order of $10^{10}$ cluster amplitudes, this is an expense, that we would like to avoid. Fortunately, there is a way around it using the inexact Newton Raphson method xv.
The Inexact Newton Raphson method
Let’s look closer at ${\bf \Omega }$ and its Jacobian ${\partial \Omega_\mu / \partial t_\nu}$:
\begin{align}
{\bf \Omega }({\bf t}) =& \langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle \\
=& \langle \mu \lvert \text{exp} \left( – \sum_\nu t_\nu \cdot \tau_\nu \right) \cdot H \cdot \text{exp} \left( \sum_\nu t_\nu \cdot \tau_\nu \right) \lvert \text{HF} \rangle
\end{align}
And for its Jacobian we have:
\begin{align}
\frac{\partial \Omega_\mu({\bf t})}{\partial t_\nu} =& \langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \tau_\nu \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle \\
& – \langle \mu \lvert \text{exp} \left( -T \right) \cdot \tau_\nu \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle \\
= & \langle \mu \lvert \text{exp} \left( -T \right) \cdot [H, \tau_\nu] \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle \\
= & \langle \mu \lvert [H_T, \tau_\nu] \cdot \lvert \text{HF} \rangle
\end{align}
In the last equation we have used that fact, that all the $\tau_\mu, \tau_\nu$ commute.
This expression simplifies drastically, if we approximate the Hamiltonian by the Fock-matrix.
\begin{align}
F =& \sum_p \epsilon_p a^\dagger_p a_p \\
F_T =& F + \sum_\mu \epsilon_\mu \cdot t_\mu \tau_\mu
\end{align}
That is, we again neglect the dynamical correlations. This seems reasonable, as we already assumed, that the Hartree-Fock-orbitals are good zero’th approximations.
This simply gives:
\begin{align}
\frac{\partial \Omega_\mu({\bf t})}{\partial t_\nu} \approx & \epsilon_\mu \cdot \delta_{\mu, \nu}
\end{align}
Note, that $ \epsilon_\mu $ are the cumulated transition energies $ \epsilon_i $ of all the canonical orbitals in the state $ \lvert \mu \rangle $. E.g.
\begin{align}
\epsilon_{ai} =& \epsilon_a – \epsilon_i \\
\epsilon_{ai,bj} =& \epsilon_a – \epsilon_i + \epsilon_b – \epsilon_j \\
\epsilon_{ai,bj,ck} =& \epsilon_a – \epsilon_i + \epsilon_b – \epsilon_j + \epsilon_c – \epsilon_k \\
\ldots
\end{align}
3.3 Møller-Plesset and Coupled Cluster Pertubation Theory in quantum chemistry
The truncation of the coupled cluster equations to single and double excitations CCSD or single, double and triple excitations CCSDT introduce a natural expansion framework and in appendix 3 we have derived concrete equation which we may solve self consistently or via the Newton Raphson methods.
But so far we have successfully ignored an important question: Is this really a systematic approximation in terms of accuracy compared to the true electron correlations?
The answer will be: Yes, but we need to add another ingredient — the coupled cluster pertubations. This will lead us to the “gold standard” of quantum chemistry in terms of quality and efficiency: The coupled cluster method with single and double excitations and pertubed triples CCSD(T). But before we briefly outline coupled cluster pertubation theory, we will sketch another, related Post-Hartree-Fock pertubation-method: The Møller Plesset perturbation theory.
Both types of pertubation methods borrough concepts from Rayleigh-Schrödinger pertubation theory. Here, the trick is, to split the Hamiltonian into a known part and a (small) pertubed potential $\lambda \cdot \Phi$. The known part is the zeroth order pertubation. Then we may iteratively expand the wavefunction and the energy in terms of the pertubation order $\lambda^n$.
Of course, in our cases, the known, unpertubed Hamiltonian will again be Fock operator $ H^{(0)} = F $. $\Phi$ is called the fluctuation potential and contains all the rest of the exact Hamiltonian:
\begin{align}
H =& \sum_{p,q} h_{pq} \cdot a^\dagger_p a_q +
\frac{1}{2} \sum_{p,q,r,s} g_{pqrs} \cdot a^\dagger_p a^\dagger_r a_q a_s \\
F =& \sum_p \epsilon_p a^\dagger_p a_p \\
H =& H^{(0)} + \lambda \cdot \Phi = F + \lambda \cdot \Phi \\ \\
& \text{and for the eigenstates} \\ \\
\lvert \psi_i \rangle =& \lvert \psi_i^{(0)} \rangle + \lambda \lvert \psi_i^{(1)} \rangle + \lambda^2 \lvert \psi_i^{(2)} \rangle + \ldots \\
E_i =& E_i^{(0)} + \lambda E_i^{(1)} + \lambda^2 E_i^{(2)} + \ldots \\
\end{align}
Møller-Plesset perturbation theory (MPT)
We know, that the zeroth order solutions are the Hartree-Fock solutions. Using those, we are able to collect all terms to any order of $\lambda^n$ in the Schrödinger equation and iteratively solve it:
\begin{align}
F \cdot \lvert \psi_i^{(0)} \rangle = & E_i^{(0)} \cdot \lvert \psi_i^{(0)} \rangle & \lambda^0 \text{ order} \\
\Phi \cdot \lvert \psi_i^{(0)} \rangle + F \cdot \lvert \psi_i^{(1)} \rangle = & E_i^{(1)} \cdot \lvert \psi_i^{(0)} \rangle + E_i^{(0)} \cdot \lvert \psi_i^{(1)} \rangle & \lambda^1 \text{ first order} \\
\left( F – E_i^{(0)} \right) \cdot \lvert \psi_i^{(1)} \rangle = & \left( E_i^{(1)} – \Phi \right) \cdot \lvert \psi_i^{(0)} \rangle & \lambda^1 \text{ first order} \\
\left( F – E_i^{(0)} \right) \cdot \lvert \psi_i^{(2)} \rangle = & \left( E_i^{(1)} – \Phi \right) \cdot \lvert \psi_i^{(1)} \rangle + E_i^{(2)} \cdot \lvert \psi_i^{(0)} \rangle & \lambda^2 \text{ second order} \\
\ldots
\end{align}
To solve the first order equation, we expand the first order wavefunction in the zeroth order basis, which we already know:
\begin{align}
\lvert \psi_i^{(1)} \rangle = \sum_j C^{(1)}_{ij} \cdot \lvert \psi_j^{(0)} \rangle
\end{align}
Substituting this into the first order equation, we get
\begin{align}
\sum_{j \neq i} C^{(1)}_{ij} \cdot \left( F – E_i^{(0)} \right) \lvert \psi_j^{(0)} \rangle =& \left( E_i^{(1)} – \Phi \right) \lvert \psi_i^{(0)} \rangle
\end{align}
If we multiple this equation by $ \langle \psi_i^{(0)} \lvert $ and re-use this result in the previous expansion, we get
\begin{align}
E_i^{(1)} =& \langle \psi_i^{(0)} \lvert \Phi \lvert \psi_i^{(0)} \rangle \\
C^{(1)}_{ij} =& – \frac{\langle \psi_j^{(0)} \lvert \Phi \lvert \psi_i^{(0)} \rangle}{E_j^{(0)} – E_i^{(0)}} \\
\lvert \psi_i^{(1)} \rangle =& – \sum_{j \neq i} \frac{\langle \psi_j^{(0)} \lvert \Phi \lvert \psi_i^{(0)} \rangle}{E_j^{(0)} – E_i^{(0)}}
\end{align}
Now, we have solved the first order equation using the zeroth order solutions. Likewise, we may proceed for the second order equations. This gives us
\begin{align}
E_i^{(2)} =& -\sum_{j \neq i} \frac{\langle \psi_i^{(0)} \lvert \Phi \lvert \psi_j^{(0)} \rangle \cdot \langle \psi_j^{(0)} \lvert \Phi \lvert \psi_i^{(0)} \rangle}{E_i^{(0)} – E_j^{(0)}} \\
\ldots
\end{align}
If you ask yourself: Very nice, but where the heck is this order parameter $\lambda$ in our electronic structure Hamiltonian?
If you look closely, you will note, that we actually don’t explicitely need an order parameter. An explicite parameter garantuees convergence, but to derive the solutions for all orders, all we needed, was the definition of the zeroth order solutions.
This finishes our discussion for second order Møller-Plesset MP2. For higher order Møller-Plesset methods more sums and products of additional fractions are introduced xvi.
In particular, the Møller-Plesset method is used for calculating the dynamical electron correlations in methods which focus on static correlations, like MSCF.
Coupled cluster perturbation theory (CCPT)
For coupled cluster perturbation theory, we start again with the similarity transformed Schrödinger equation:
\begin{align}
\text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& E \cdot \lvert \text{HF} \rangle \\
\left( F_T + \Phi_T \right) \lvert \text{HF} \rangle =& E \cdot \lvert \text{HF} \rangle
\end{align}
We now expand according to
\begin{align}
T =& \sum_n T^{(n)} \quad & \Phi_T =& \sum_n \Phi_T^{(n)} \\
=& \sum_n \sum_\mu t^{(n)}_{\mu} \cdot \tau_{\mu} \\
E =& \sum_n E^{(n)} & F_T =& F + \sum_n \sum_\mu \epsilon_\mu t_\mu^{(n)} \cdot \tau_\mu
\end{align}
Here, we have assumed an implicite pertubation parameter $\lambda$ which is hidden in the individual terms.
Note that these are expansions in the pertubation orders of the electron correlations and not an expansion in coupled cluster excitation orders. E.g. we have
\begin{align}
T_2 =& \sum_n T_2^{(n)}
\end{align}
If we again collect terms to all pertubation orders and proceed similar to our derivation of the coupled cluster equations, we get
\begin{align}
E^{(n)} =& \langle \text{HF} \lvert \Phi_T^{(n)} \lvert \text{HF} \rangle \\
\epsilon_\mu \cdot t_\mu^{(n)} =& \langle \mu \lvert \Phi_T^{(n)} \lvert \text{HF} \rangle
\end{align}
Now, we apply the Baker-Campbell-Hausdorff expansion again, as for the energy expression in appendix 3, this time for the similarity transformed fluctuation potential:
\begin{align}
\Phi_T =& \Phi + [\Phi,T] + \frac{1}{2!} [[\Phi,T],T] + \frac{1}{3!} [[[\Phi,T],T],T] \\ & + \frac{1}{4!} [[[[\Phi,T],T],T],T] + \cdots
\end{align}
Next, we use the expansion of $T$ to all pertubation orders and collect terms, we get
\begin{align}
\epsilon_\mu \cdot t_\mu^{(1)} =& \langle \mu \lvert \Phi \lvert \text{HF} \rangle \\
\epsilon_\mu \cdot t_\mu^{(2)} =& \langle \mu \lvert [\Phi,T^{(1)}] \lvert \text{HF} \rangle \\
\epsilon_\mu \cdot t_\mu^{(3)} =& \langle \mu \lvert [\Phi,T^{(2)}] \lvert \text{HF} \rangle – \langle \mu \lvert [[\Phi,T^{(1)}],T^{(1)}] \lvert \text{HF} \rangle \\
\cdots
\end{align}
Note, that this is indeed the right order matching as a single $ \Phi $ is the first order correction, just as in Møller-Plesset theory. Further notice, that the cluster amplitudes $ t_\mu $ appear on both sides of the equations: As $ \epsilon_\mu \cdot t_\mu^{(\ldots)} $ on the left hand side and also in the expansions of $ T^{(\ldots)} = \sum_\mu t_\mu^{(\ldots)} \cdot \tau_\mu $ on the right hand side.
Up to this point, we should assume, that all excitations levels of $\mu$ may contribute to each pertubation order of $ T^{(\ldots)} $. But the structure of the the iterative pertubation scheme and the individual commutators above imposes constraints on the type of excitation levels, that contribute to each term on the right hand side. This will give us a connection of cluster excitations and pertubation orders:
$ \Phi $ can excite at most 2 electrons. So, to first pertubation order only double excitations contribute. Single excitations don’t contribute, because of the Brillouin-theorem.
\begin{align}
\epsilon_{\mu_2} \cdot t_{\mu_2}^{(1)} =& \langle \mu_2 \lvert \Phi \lvert \text{HF} \rangle \\
\lvert \text{CC}^{(1)} \rangle =& \text{exp}(T)^{(1)} \lvert \text{HF} \rangle \\
=& T_2^{(1)} \lvert \text{HF} \rangle
\end{align}
Specifically, we have $ T^{(1)} = T_2^{(1)} $. To second pertubation order only singles, doubles and triples excitations contribute to the wavefunction, since $ [\Phi,T^{(1)}] = [\Phi,T_2^{(1)}] $ can excite at most three electrons (for details see our remarks in appendix 3).
To third pertubation order also quadruple excitations contribute. Also, to third pertubation order additional higher order corrections to the singles, doubles and triples amplitudes are present in the equation for $ \epsilon_\mu \cdot t_\mu^{(3)} $.
In general $n$th level excitations contribute to pertubation order $n-1$. This is kind of bad news for the CCSD truncation, because this indicates, that we cannot reach second pertubation order by using it. But we will see, how we can improve this.
What about the energy? So far, our equation for $ E^{(n)}$ apparently requires the knowledge of the amplitudes up to $ t_\mu^{(n-1)}$
\begin{align}
E^{(n)} =& \langle \text{HF} \lvert \Phi_T^{(n)} \lvert \text{HF} \rangle
\end{align}
Now, there is a this very useful theorem by Eugene Wigner, that corrects this assumption:
3.4 CCSD(T): The “gold standard” of Quantum Chemistry
The “2n+1 rule” states, that in order to calculate the $ E^{(2n+1)} $ corrections, we only need the knowledge of the wavefunction up to the pertubation order of $n$.
This result is actually pretty nice: It means, using the amplitudes to second pertubation order, will give us the energy up to fifth pertubation order!
I sketch the derivation of CCSD(T) in more detail in the
Appendix 4: Derivation of the CCSD(T) equation and here I summarize the results:
The appendix 4 shows: The CCSD single and double amplitudes are correct to second pertubation order. So much for the good news. But unfortunately, they don’t represent a good approximation of the actual wavefunction up to second pertubation order. In order to reach this, we have to include the second order triple excitations. Thus, if we could also take these into account, we would be able to calculate the energy up to 4th and 5th pertubation order!
As indicated in the appendix 4, the exact equations for this turn out to be very hard and the CCSD(T) method now chooses a middle way.
For one thing, second order triples amplitudes are approximated from the CCSD $T_2$ amplitudes. Next, from the energy corrections, we only consider those terms in $E_\text{trip}^{(4)}, E_\text{trip}^{(5)} $ that depend on the single and double excitations.
Finally this gives the following correction to CCSD:
\begin{align}
\Delta E_\text{CCSD(T)} =& \sum_{\mu_1} \bar{t}_{\mu_1} \cdot \langle \mu_1 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle + \sum_{\mu_2} \bar{t}_{\mu_2} \cdot \langle \mu_2 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle
\end{align}
The new parameters $ \bar{t}_{\mu} $ are additional Lagrange-parameters, the are introduced along the derivation.
Limits of the CCSD(T) method
We already got an impression how far FCI and CASCF may be scaled on current digital hardware. For CCSD(T) among the largest calculation ever performed are xvii:
- In the year 2010: A ${H_2O}_{17}$ cluster in the aug-cc-pVTZ basis set, which corresponds to 128 electrons and 1564 orbitals, using a frozen core approximation.
- A similar ${H_2O}_{16}$ calculation was executed on 120 000 computer cores and took more than 3 hours in 2010.
- In 2020: The energy of 2-aminobenzophenone ($ABP, C_{13}H_{11}NO$) was computed. This calculation, utilizing the density-fitting approximation, correlated 90 electrons among 1569 orbitals and was completed on 224 computer cores in 68 hours.
3.5 The scaling of Post-Hartree-Fock methods
We arrive at an overview of the scaling of the different Post-Hartree-Fock methods, that I have introduced so far ($N$ being the number of basis functions) xviii:
| $N^5$ | MP2 |
| $N^6$ | MP3, CISD < CCSD (better quality) |
| $N^7$ | MP4, CCSD(T) |
| $N^8$ | MP5, CISDT, CCSDT |
| $N^9$ | MP6, CCSDT(Q) |
| $N^{10}$ | MP7, CISDTQ, CCSDTQ |
3.6 The Density Matrix Renormalization Group (DMRG) in Quantum Chemistry
Before we end our quick tour through Post-Hartree-Fock methods I want to just mention one more strategy, that has become increasingly relevant during the last couple of decades. The density matrix renormalization group (DMRG) method is different compared to other electronic structure theories in quanutm chemistry. But as being a tensor network strategy its concept is probably much more familiar to the quantum computing community.
There are excellent introductions out there, so I will just touch this topic here. In this section I follow the nice pedagogical overview and survey of concrete calculations in quantum chemistry by Chan and Sharma xix. For an in-depth introduction see the work by Wouters and Van Neck xx.
Again, our starting point is the occupation number representations of the canonical molecular orbitals. This time, we sum up occupation numbers in terms of the spatial orbitals. A general full CI expansion of a molecule’s state reads:
\begin{align}
\lvert \Psi \rangle &= \sum_{n_1 \ldots n_k} \Psi^{n_1 n_2 n_3 \ldots n_k} \lvert n_1 n_2 n_3 \ldots n_k \rangle \\
& \text{with} \\
\{n_i\} &= \{\lvert \text{vac} \rangle, \lvert \uparrow \rangle, \lvert \downarrow \rangle, \lvert \uparrow \downarrow \rangle \}
\end{align}
Matrix Product State (MPS)
Again, our goal is to vary the coefficients $ \Psi^{n_1 n_2 n_3 \ldots n_k} $ and minimize the expectation value of our Hamiltonian. Of course, this will scale exponentially in $k$. Thus, we start to simplify the coefficients $ \Psi^{n_1 n_2 n_3 \ldots n_k} $:
We may interpret $ \Psi^{n_1 n_2 n_3 \ldots n_k} $ as a tensor with $k$ open indices. We could simplify this tensor by a simple product ansatz:
\begin{align}
\Psi^{n_1 n_2 n_3 \ldots n_k} &\approx \Psi^{n_1} \Psi^{n_2} \Psi^{n_3} \Psi^{n_k}
\end{align}
As this will give us poor results, we add more flexibility, by turning the simple coefficients into $M \times M$ -matrices
\begin{align}
\Psi^{n} \rightarrow \Psi^{n}_{i i’} =: A^{n}_{i i’}
\end{align}
and the scalar products into matrix products:
\begin{align}
\Psi^{n_1 n_2 n_3 \ldots n_k} &\approx A^{n_1} \cdot A^{n_2} \cdot A^{n_3} \cdots A^{n_k}
\end{align}
This matrix product state reduces the order of the exponential tensor of full CI to $O(4M^2k)$.
As this ansatz introduces a one dimensional chain of correlations between adjacent “sites” $A^n, A^{n+1}$, we may expect it to fit well for “quasi one-dimensional” problem structures. Even more precise: The singular value decomposition ensures, that we may decompose every $m \times n $-matrix into two unitary matrices $U, V$ and a real and positive, diagonal $m \times n $-matrix in the middle $A = U \cdot D \cdot V^{-1}$.
Using this we iteratively split site by site from the tensor $\Psi^{n_1 n_2 n_3 \ldots n_k}$ as illustrated in this diagramm:
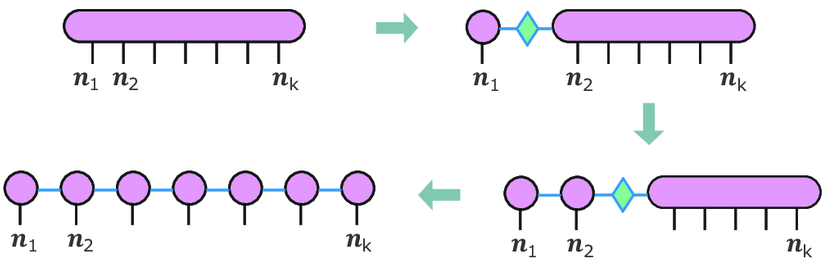
https://www.researchgate.net/publication/370752149_Photo-processes_in_biology_A_glimpse_from_computational_chemistry_and_machine_learning_Light_matter_interaction
As such a general SVD is precise, the size of the components must grow exponentially from left to right. But we may simplify the decomposition by introducing a bond dimension $M$ , cut-off of the smallest entries of $ D $, in each iteration. This is actually the same as cutting-off the Schmidt-rank of the composite systems. Typical ranges are e.g. $ 300 \leq M \leq 5000$, while increasing $M$ is able to capture more and more details of the true wavefunction.
Note, that the bond dimension is a cut-off for the inner indices $i$. The physical, outer indices $n$ are untouched by this.
The Renormalized Canonical Form
The structure of the matrix product state allows us, to apply a few symmetry transformations, that leave the state invariant. Thus, we may introduce a canonical form by tayloring local $X \cdot X^{-1}$ insertions between sites, with the following goal:
\begin{gather}
\lvert \Psi \rangle = \sum_{n_1 \ldots n_k} L^{n_1} \cdots L^{n_{p-1}} \cdot C^{n_p} \cdot R^{n_{p+1}} \cdots R^{n_{n_k}} \lvert n_1 n_2 n_3 \ldots n_k \rangle \\
\text{with the orthogonality conditions} \\
\sum_n {L^n}^\dagger \cdot L^n = 1 \\
\sum_n R^n \cdot {R^n}^\dagger = 1
\end{gather}
This may be interpreted as a transformation into the new renormalized many-particle basis states $\{l\}$ and $\{r\}$:
\begin{align}
\lvert l_i \rangle :=& \sum_{ \{n\} } [ L^{n_1} \cdots L^{n_{p-1}} ]_i \lvert n_1 n_2 \ldots n_{p-1} \rangle \\
\lvert r_i \rangle :=& \sum_{ \{n\} } [ R^{n_{p+1}} \cdots R^{n_k} ]_i \lvert n_{p+1} \ldots n_k \rangle \\
\end{align}
Using this new, smaller basis our matrix product state reduces to
\begin{gather}
\lvert \Psi \rangle = \sum_{l, n, r} C^{n_p}_{l,r} \lvert l, n_p, r \rangle
\end{gather}
Variation and the sweeping algorithm
The variation strategy of the expectation value $ \langle \Psi \lvert H \lvert \Psi \rangle $ in DMRG is visualized very nicely on tensornetwork.org xxi:
For the iterative sweeping algorithm , we start with two adjacent sites, that we want to optimize and leave the other sites fixed.
On tensornetwork.org, these are just the first two sites. As the Hamiltonian is given in second quantization, it may be expressed as a matrix product operator . To derive the expectation value, we first “sandwich” the Hamiltonian between two copies of the matrix product states $ \Psi $. Next, we generate an effective Hamiltonian $H_\text{eff}$ for the first to sites, by contracting all the indices / inner lines of the other sites in this sandwich:
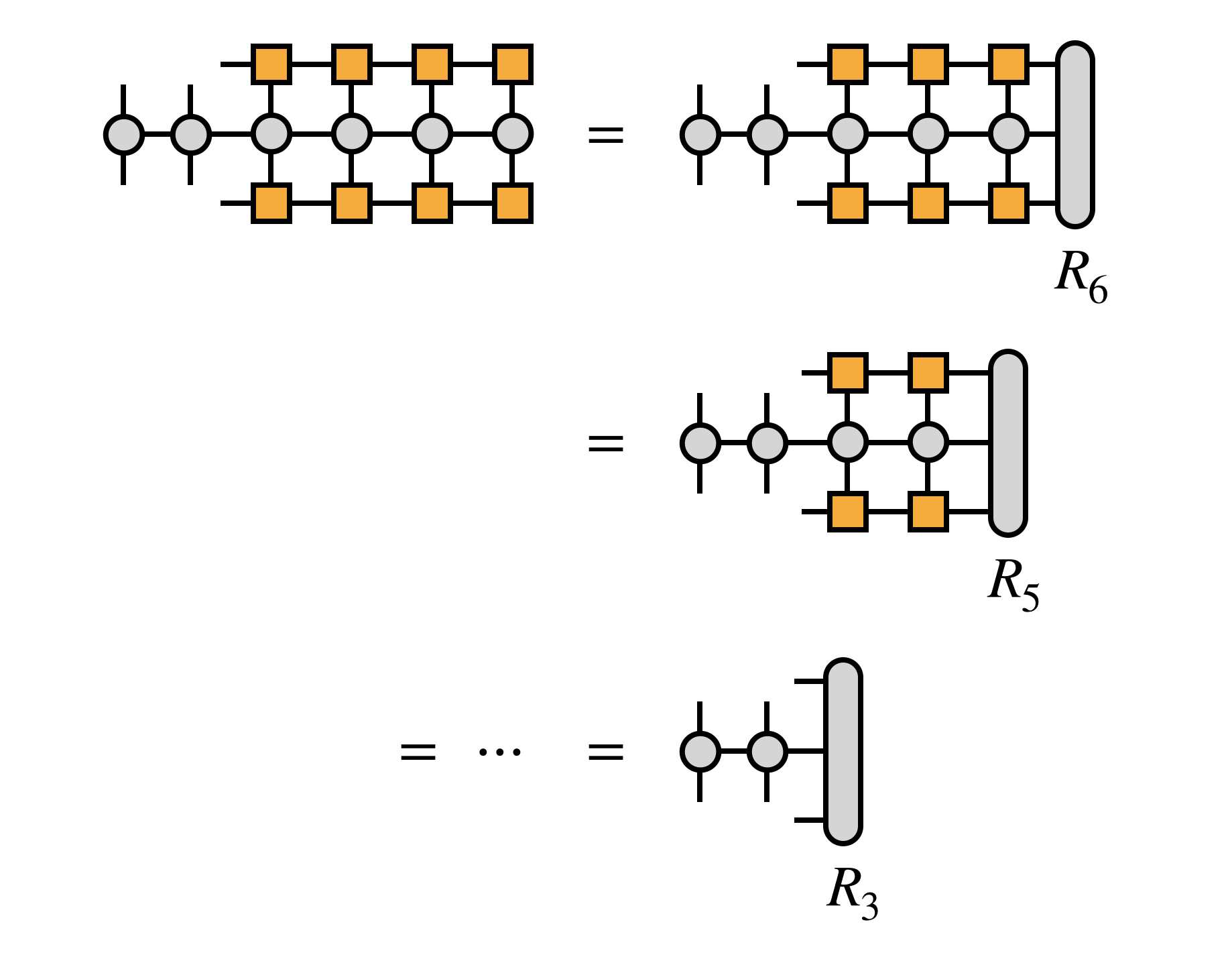
https://tensornetwork.org/mps/algorithms/dmrg/
Using this effective Hamiltonian, we may optimize the combined two-sited state
\begin{gather}
B^{n_1 n_2} = A^{n_1} \cdot A^{n_2}
\end{gather}
Here we have used our original notation $A^{n_i}$ but keep in mind, that these tensors are transformed into the normal form.
The optimization is done, by approximately diagonalizing $H_\text{eff} \cdot B^{n_1 n_2}$. This may be achieved by well-known iterative eigensolver algorithms. At this stage, an approximate solution is enough, because for reaching accuracy, we first have to take care of all the other sites:
For this, the optimized first two sites $ \tilde{B}^{n_1 n_2}$ are again decomposed by another SVD followed by the truncation of the bond dimension. The features of the SVD ensures, that the new $A^{n_i}$ are already in normal form. For the next iteration, we proceed our optimization for the sites $ A^{n_2} \cdot A^{n_3} $.
Using these micro iterations, our algorithm sweeps from left to right and back, until we reach a predefined level of self consistency.
By the way, what has this all to do with “density matrices” as the name DMRG indicates? In the original work, the micro iteration was formulated using reduced density matrices.
DMRG: Computational Limits
Using the (quasi) local properties of certain examples, DMRG is able to compute static correlations by covering a broader active space than MCSCF. We have stated the example of a $Cr_3$-calculation using a (20, 20)-CAS by exploiting parallel computation. In contrast Chan and Sharma cite a near-exact DMRG-calculation of the $Cr_2$-molecule using an active space of (24, 30).
The work also describes examples of much larger one dimensional molecules. E.g. the simultaneous bond-breaking of 49 bonds in a hydrogen chain, a problem nominally requiring an active space of (50, 50), a Hilbert space of $10^{28}$ Slater determinants.
6 Appendices
6.1 Appendix 2: The orbital optimization in MCSCF
In the main text, you saw a detailed expression of the energy function for MCSCF along with a whole bunch of defintions. For the orbital optimization we parametrize this energy function using the rotations $R_{rk}$. Here, I summarize the expressions for the gradient and the Hessian with respect to these rotations. I recommend, that you open another browser window for the definitions in the main text, as I will not repeat them here.
The rotations $R_{ij}$ between inactive orbitals and $R_{ab}$ between virtual orbitals are $=0$ since the energy is independent to these rotations.
One may actually insert this expansion into the energy formula and sort it by linear and quadratic terms in the orbital rotation generators $R_{rk}$. Note, for instance, that the closed-shell energy $E_c$ is not effected by $R$, since the rotations do not effect inactive orbitals. For the same reason, we only have to examine the transformation of the active indices in the closed-shell Fock matrix $F_{rs}^c$. Also, we will have to check, how the active one- and two-particle reduced density matrices transform via the expansion of $exp(R)$ using the anticommutator rules. E.g.
\begin{align}
D_{tu} = \sum_{IJ} c_I \cdot \gamma^{IJ}_{tu} \cdot c_J \rightarrow \sum_{IJ} c_I \cdot \langle \Phi_I \lvert exp(-R) \cdot E_{tu} \cdot exp(R) \lvert \Phi_J \rangle \cdot c_J
\end{align}
All in all one gets, by introducing new tensors $A$ and $G$ (see below):
\begin{align}
E^{(2)}(R) = E_0 + 2 \sum_{rk} A_{rk} \left( R_{rk} + \frac{1}{2}\left(R^2\right)_{rk} \right) +
\sum_{rk, sl} R_{rk} \cdot G_{rs}^{kl} \cdot R_{sl}
\end{align}
The gradient $g_{rk}$ and the Hessian $h_{rk,sl}$ are obtained by differentiating the energy $E^{(2)}(R) $ with respect to $R$ and evaluating the terms for $R = 0$ afterwards. By introducing the permutation operator $\pi$ with $ \pi_{rk}A_{rk} = A_{kr}$, one finally gets
\begin{align}
g_{rk} = 2 \left(1 − \pi_{rk} \right) A_{rk} = 2 \left( A_{rk} – A_{kr} \right)
\end{align}
and
\begin{align}
h_{rk,sl} = \left(1 − \pi_{rk} \right) \left(1 − \pi_{sl} \right)
\left( G_{rs}^{kl} – \delta_{kl} \left( A_{rs} + A_{sr} \right) \right)
\end{align}
\begin{align}
A_{ri} = 2F_{ri}, \quad
A_{rt} = \sum_u^{\text{act}} F_{ru}^c \cdot D_{ut} +
\sum_{uvw} J_{ru}^{vw} \cdot D_{tu, vw}, \quad
A_{rt} = 0
\end{align}
$F_{rs}$ is known as the general Fock matrix, and it is built from the closed-shell Fock matrix $F_{rs}^c$
\begin{align}
F_{rs} = \sum_{tu} D_{tu} \left(J^{tu}_{rs} – \frac{1}{2} K^{tu}_{rs}\right)
\end{align}
For the Hessian we need the G-tensor:
\begin{align}
G^{ij}_{rs} =& 2 \left(F_{rs} \delta_{ij} + L^{ij}_{rs} \right) \\
G^{tj}_{rs} =& \sum_v^{\text{act}} D_{tv} L^{vj}_{rs} =
G^{jt}_{sr} \\
G^{tu}_{rs} =& F^c_{rs} D_{tu} + \sum_{vw}^{\text{act}}
D_{tu, vw} + 2 K^{vw}_{rs} \cdot D_{tv, uw}
\end{align}
with
\begin{align}
L^{kl}_{rs} = 4 K^{kl}_{rs} – K^{lk}_{rs} – J^{kl}_{rs}
\end{align}
Finally!
6.2 Appendix 3: Simplifying the Coupled Cluster Equations
Using the similarity transformed Hamiltionian we derived the coupled cluster equations:
\begin{align}
\langle \text{HF} \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& E & \text{(1)} \\
\langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& 0 & \text{(2)}
\end{align}
We may get rid off the exponentials by using the commutations rules of the well-known Baker-Campbell-Hausdorff expansion:
\begin{align}
H_T =& H + [H,T] + \frac{1}{2!} [[H,T],T] + \frac{1}{3!} [[[H,T],T],T] \\ & + \frac{1}{4!} [[[[H,T],T],T],T] + \cdots
\end{align}
If we look closer at those commutators, we see, that each commutator reduces the length of the $a^\dagger_a a_i $ strings, compared to the simple product. E.g.
\begin{align}
[a^\dagger_a a_i, a^\dagger_b a_j] = \delta_{i,b} a^\dagger_a a_j − \delta_{a,j} a^\dagger_b a_i
\end{align}
This means, as $H$ is a one and two particle operator, four successive commutations removes the contributions from $H$. Thus, the BCH-expansion above already terminates after the fourth term.
This gives us the coupled cluster equations:
\begin{align}
E =& \quad \langle \text{HF} \lvert H \lvert \text{HF} \rangle
+ \langle \text{HF} \lvert [H,T] \lvert \text{HF} \rangle \\
& + \frac{1}{2!} \langle \text{HF} \lvert [[H,T],T] \lvert \text{HF} \rangle \\
& + \frac{1}{3!} \langle \text{HF} \lvert [[[H,T],T],T] \lvert \text{HF} \rangle \\
& + \frac{1}{4!} \langle \text{HF} \lvert [[[[H,T],T],T],T] \lvert \text{HF} \rangle
\end{align}
This simplifies considerably: $T$ does only produce excited states, so $\langle \text{HF} \lvert T = 0 $. Again, as $H$ is a one and two particle operator, it can de-excite at most 2 electrons. Thus $\langle \text{HF} \lvert H T_i \lvert \text{HF} \rangle = 0 $ for $ i>2$.
This gives us the energy expression:
\begin{align}
E = E_\text{HF} + \langle \text{HF} \lvert [H,T_2] \lvert \text{HF} \rangle +
\frac{1}{2} \langle \text{HF} \lvert [[H,T_1],T_1] \lvert \text{HF} \rangle
\end{align}
Thus, the energy depends directly only on the amplitudes of single and double excitations. But these amplitudes still depend on all the other amplitudes in a non-linear way:
\begin{align}
0 =& \quad \langle \mu \lvert H \lvert \text{HF} \rangle
+ \langle \mu \lvert [H,T] \lvert \text{HF} \rangle \\
& + \frac{1}{2!} \langle \mu \lvert [[H,T],T] \lvert \text{HF} \rangle \\
& + \frac{1}{3!} \langle \mu \lvert [[[H,T],T],T] \lvert \text{HF} \rangle \\
& + \frac{1}{4!} \langle \mu \lvert [[[[H,T],T],T],T] \lvert \text{HF} \rangle
\end{align}
In the main text, we analyze this amplitude equation further.
6.3 Appendix 4: Derivation of the CCSD(T) equation
The “2n+1 rule” states, that in order to calculate the $ E^{(2n+1)} $ corrections, we only need the knowledge of the wavefunction up to the pertubation order of $n$. The prove is also sketched in the script of W. Klopper and D. Tew. You may also find an explanation in this video-channel xxii.
For the “2n+1”-rule, we interpret the coupled cluster equations as a minimization problem of the energy subject to the constraint that the amplitudes fulfill the projected amplitude equation:
\begin{align}
\langle \text{HF} \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& E \\
\langle \mu \lvert \text{exp} \left( -T \right) \cdot H \cdot \text{exp} \left( T \right) \lvert \text{HF} \rangle =& 0
\end{align}
For this, just as for the derivation of the Hartree-Fock method, we introduce additional Lagrange parameters $\bar{t}_\mu$ and minimize the following Lagrange-function :
\begin{align}
L(t, \bar{t}) = \langle \text{HF} \lvert F_T + \Phi_T \lvert \text{HF} \rangle + \sum_\mu
\bar{t}_\mu \cdot \langle \mu \lvert F_T + \Phi_T \lvert \text{HF} \rangle
\end{align}
Again, we may expand the coupled cluster Lagrangian to all perturbation orders. This gives us a minimization problem to each pertubation order. Using this, one is able to eliminate all variables $t_\mu, \bar{t}_\mu$, that appear linearly in each $ L^{(2n)} $ and $ L^{(2n+1)} $. This is the case for all $\bar{t}_\mu^{(k)}$ and $t_\mu^{(k)}$ with $ k>n $.
This gives an energy expression $ E^{(2n+1)} $ that only depends on $\bar{t}_\mu^{(k)}$ and $t_\mu^{(k)}$ with $ k \le n $.
This result is actually pretty nice: It means, using the amplitudes $t_\mu^{(k)}, \bar{t}_\mu^{(k)}$ to second pertubation order, will give us the energy up to fifth pertubation order!
Using the results from the Lagrangian-minization one may analyze, how excitation levels and pertubation orders are related to each other. Recall, that the n-tuple excitations $t_{\mu_n}$ first appeared at pertubation order $n-1$. What happens to the amplitude expansions, if we include $ t_{\mu_n}$ in the coupled cluster equations?
The inclusion effects the amplitudes $ t_{\mu_{n-1}}$ and $ t_{\mu_{n-2}}$ directly. Their corrections are of pertubation order $n$. The lower excitation amplitudes are effected indirectly through the changes of $ t_{\mu_{n-1}}$ and $ t_{\mu_{n-2}}$. These corrections are of higher pertubation order $n+1$.
This shows: The CCSD single and double amplitudes are correct to second pertubation order. So much for the good news. But unfortunately, they don’t represent a good approximation of the real wavefunction up to second pertubation order. In order to reach this, we have to include the second order triple excitations. Thus, if we could also take these into account, we would be able to calculate the energy up to 4th and 5th pertubation order! The expressions for the corrections finally read as follows:
\begin{align}
E_\text{trip}^{(4)} =& \sum_{\mu_2} \bar{t}_{\mu_2}^{(1)} \cdot \langle \mu_2 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle \\
E_\text{trip}^{(5)} =& \sum_{\mu_1} \bar{t}_{\mu_1}^{(2)} \cdot \langle \mu_1 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle + \sum_{\mu_2} \bar{t}_{\mu_2}^{(2)} \cdot \langle \mu_2 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle \\
+& \sum_{\mu_3} \bar{t}_{\mu_3}^{(2)} \cdot \langle \mu_3 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle + \sum_{\mu_4} \bar{t}_{\mu_4}^{(2)} \cdot \langle \mu_4 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle \\
+& \sum_{\mu_3} \bar{t}_{\mu_3}^{(2)} \cdot \langle \mu_3 \lvert [\Phi, T^{(2)}] \lvert \text{HF} \rangle + \frac{1}{2}\sum_{\mu_3} \bar{t}_{\mu_3}^{(2)} \cdot \langle \mu_3 \lvert [[\Phi, T_2^{(1)}],T_2^{(1)}] \lvert \text{HF} \rangle
\end{align}
CCSD(T) now makes the following simplification: For one thing, second order triples amplitudes are generated from the CCSD $T_2$ amplitudes. Next, from the energy correction above, we only consider the first two terms in $ E_\text{trip}^{(5)} $ as we already know the single and double excitations, while the triples and quadruples amplitudes are too hard to compute. This is definitely an improvement to CCSD, although not as good as the real correction to 5th pertubation order:
\begin{align}
\Delta E_\text{CCSD(T)} =& \sum_{\mu_1} \bar{t}_{\mu_1} \cdot \langle \mu_1 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle + \sum_{\mu_2} \bar{t}_{\mu_2} \cdot \langle \mu_2 \lvert [\Phi, T_3^{(2)}] \lvert \text{HF} \rangle
\end{align}
Finally!
7 Footnotes
i https://www.ipc.kit.edu/theochem/download/Kapitel2.pdf: “Second quantization”, lecture notes by Wim Klopper and David P. Tew, 2006 University of Karlsruhe KIT
iii https://arxiv.org/abs/1812.09976: “Quantum Chemistry in the Age of Quantum Computing” (2018), by Yudong Cao, Jonathan Romero, Jonathan P. Olson, Matthias Degroote, Peter D. Johnson, Mária Kieferová, Ian D. Kivlichan, Tim Menke, Borja Peropadre, Nicolas P. D. Sawaya, Sukin Sim, Libor Veis, Alán Aspuru-Guzik
iv https://arxiv.org/abs/quant-ph/9703054: “Simulation of Many-Body Fermi Systems on a Universal Quantum Computer” Daniel S. Abrams (1), Seth Lloyd (2) 1997
v https://arxiv.org/abs/quant-ph/0604193: “Simulated Quantum Computation of Molecular Energies” Alán Aspuru-Guzik, 2006
vi https://arxiv.org/abs/1001.3855: “Simulation of Electronic Structure Hamiltonians Using Quantum Computers”
James D. Whitfield (2010)
vii https://pennylane.ai/qml/demos/tutorial_measurement_optimize/: “Measurement optimization”, by the PennyLane-team
viii https://journals.aps.org/prresearch/abstract/10.1103/PhysRevResearch.4.033154#fulltext: “Measurements as a roadblock to near-term practical quantum advantage in chemistry: Resource analysis” by J. Gonthier, M. Radin, C. Buda, E. Doskocil, C. Abuan, and J. Romero, Phys. Rev. Research (2022)
ix https://elib.uni-stuttgart.de/bitstream/11682/11666/3/Dissertation_DavidKreplin.pdf: “Multiconfiguration self-consistent field methods for large molecules”, David Amos Kreplin, 2020 University of Stuttgart
x https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Quantum_Mechanics__in_Chemistry_(Simons_and_Nichols): “Quantum Mechanics in Chemistry” chapter 18
by Simons and Nichols University of Utah
xi In “Quantum Mechanics in Chemistry” chapter 18, you will find the following informal description of the reduced density matrices:
\begin{align}
D_{tu} := \sum_{IJ} c_I \cdot \gamma^{IJ}_{tu} \cdot c_J
\quad \text{ and } \quad
D_{tuvw} := \sum_{IJ} c_I \cdot \Gamma^{IJ}_{tuvw} \cdot c_J
\end{align}
-
1. $D_{tt}$ : The sum over all CSFs, in which $\varphi_t$ is occupied, of the square of the CI coefficient of that CSF:
\begin{align}
D_{tt} := \sum_{I} \left( \text{with $\varphi_t$ occupied} \right) \cdot c_I^2
\end{align} -
2. $D_{tu}$ : Accordingly
\begin{align}
D_{tu} := \sum_{IJ} (sign) \left( \text{with $\varphi_t$ occupied in I and $\varphi_u$ occupied in J} \right) \cdot c_Ic_J
\end{align} -
3. $D_{tu tu}$ : Likewise
\begin{align}
D_{tu tu} := \sum_{I} \left( \text{with both $\varphi_t$ and and $\varphi_u$ occupied in I} \right) \cdot c_I^2
\end{align} -
4. $D_{tu vw}$ : … aah, let’s skip this one …
By the way, the authors there prefer the notation $ D_{tu} =: \gamma_{tu} $ and $ D_{tuvw} =: \Gamma_{tuvw} $.
xii https://pubs.aip.org/aip/jcp/article/147/18/184111/195383/Pushing-configuration-interaction-to-the-limit: “Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations”, by Konstantinos D. Vogiatzis, Dongxia Ma, Jeppe Olsen, Laura Gagliardi, Wibe A. de Jong, The Journal of Chemical Physics (2017)
xiii https://arxiv.org/abs/2009.12472: “How will quantum computers provide an industrially relevant computational advantage in quantum chemistry?”, Vincent E et al. (2020)
xiv https://www.ipc.kit.edu/theochem/download/Kapitel3.pdf: “Coupled cluster theory: Fundamentals”, by Wim Klopper and David P. Tew (University of Karlsruhe)
xv https://arxiv.org/abs/2004.07773: “Accelerated multimodel Newton-type algorithms for faster convergence of ground and excited state coupled cluster equations”, by E. Kjønstad, S. Folkestad, H. Koch
xvi https://www.chemistry.tcd.ie/assets/pdf/ss/DAMB/DAMB%20SS/PERTURBATION%20THEORY.pdf: “Rayleigh-Schrödinger Perturbation Theory” from Trinity College Dublin
xvii https://arxiv.org/abs/2009.12472: “How will quantum computers provide an industrially relevant computational advantage in quantum chemistry?”, by Vincent E et al. (2020)
xviii https://www.youtube.com/watch?v=np81k16E4I0&list=PLkNVwyLvX_TFBLHCvApmvafqqQUHb6JwF&index=18: “CompChem.04.03 Post Hartree-Fock Theory: Perturbation and Coupled Cluster Theories”, by Chris Cramer on YouTube
xix https://aiichironakano.github.io/phys516/Chan-DMRG-ARPC11.pdf: “The Density Matrix Renormalization Group in Quantum Chemistry”, by by Garnet Chan and Sandeep Sharma, University of Southern California, Annu. Rev. Phys. Chem. (2011)
xx https://arxiv.org/abs/1407.2040: “The density matrix renormalization group for ab initio quantum chemistry”, by Sebastian Wouters, Dimitri Van Neck, Ghent University (2014)
xxii https://www.youtube.com/watch?v=-U1lvDDZmPI: “The 2n+1 Theorem | Perturbation Theory | Quantum Mechanics” by the PrettyMuchPhysics-channel